题目内容
奥地利数学家皮克发现了一个计算正方形网格纸中多边形面积的公式:
S=a+
b-1,方格纸中每个小正方形的边长为1,其中a表示多边形内部的格点数,b表示多边形边界上的格点数,S表示多边形的面积.
注:①由n条线段依次首尾连接而成的封闭图形叫做n边形,这些线段的端点叫做顶点;
②网格中小正方形的顶点叫格点.
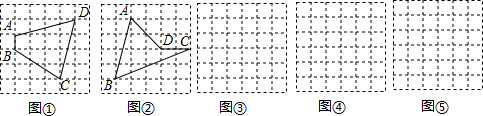
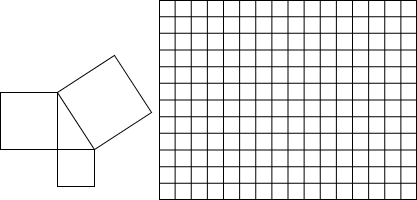
如:在图①中,点A、B、C、D都正好在格点上,那么四边形ABCD的面积S=8+
×4-1=9.
运用上述知识回答:
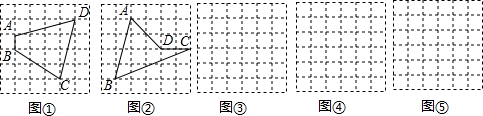
(1)如图②中,求四边形ABCD的面积;
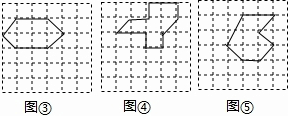
(2)如图③、④、⑤,若多边形的顶点都在格点上,且面积为6,请画出这样三个形状不同的多边形(多边形的边数≥6).并写出相应的a、b的值.
a=
b=
S=a+
| 1 |
| 2 |
注:①由n条线段依次首尾连接而成的封闭图形叫做n边形,这些线段的端点叫做顶点;
②网格中小正方形的顶点叫格点.
如:在图①中,点A、B、C、D都正好在格点上,那么四边形ABCD的面积S=8+
| 1 |
| 2 |
运用上述知识回答:

(1)如图②中,求四边形ABCD的面积;
(2)如图③、④、⑤,若多边形的顶点都在格点上,且面积为6,请画出这样三个形状不同的多边形(多边形的边数≥6).并写出相应的a、b的值.
a=
3
3
; a=1
1
; a=3
3
;b=
8
8
.b=12
12
.b=8
8
.分析:(1)通过阅读分析确定图②中的a=5,b=6,再根据S=a+
b-1就可以求出图②中四边形ABCD的面积.
(2)根据格点多边形的定义就可以在图③、图④、图⑤的图形中画出符合条件的格点六边形,从而求出a、b的值.
| 1 |
| 2 |
(2)根据格点多边形的定义就可以在图③、图④、图⑤的图形中画出符合条件的格点六边形,从而求出a、b的值.
解答:解:(1)由题意,得
a=5,b=6,
∴S=a+
b-1
=5+
×6-1
=7
(2)由图形,得
图③,a=3,b=8,
图④,a=1,b=12,
图⑤,a=3,b=8,
故答案为:3,8;1,12;3,8.
a=5,b=6,
∴S=a+
| 1 |
| 2 |
=5+
| 1 |
| 2 |
=7
(2)由图形,得
图③,a=3,b=8,
图④,a=1,b=12,
图⑤,a=3,b=8,
故答案为:3,8;1,12;3,8.

点评:本题是一道有关勾股定理的解答题,考查了格点图形的面积的计算,正方形网格纸中多边形面积的公式:S=a+
b-1的运用,勾股定理的运用,阅读理解能力的训练.
| 1 |
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 b-1,方格纸中每个小正方形的边长为1,其中a表示多边形内部的格点数,b表示多边形边界上的格点数,S表示多边形的面积.
b-1,方格纸中每个小正方形的边长为1,其中a表示多边形内部的格点数,b表示多边形边界上的格点数,S表示多边形的面积.