题目内容
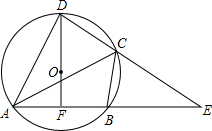已知：如图，圆内接四边形ABCD的两边AB、DC的延长线相交于点E，DF过圆心O交AB于点F，AB=BE，连接AC，且OD=3，AF=FB=| 5 |
分析：由于DF⊥AB，根据垂径定理可得出弧AD=弧BD，即∠DCA=∠DAB，因此△ADC和△EDA相似，所以本题可用形似三角形来求解．那么根据相似三角形可得出关于AC、AE、AD、DE的比例关系式，已知了圆的半径和OF的长，因此可连接OA求出FO的长，进而可在直角△ADF中求出AD的长，同理可在直角△DFE中求出DE的长，而AE=4AF，由此可求出AC的长．
解答：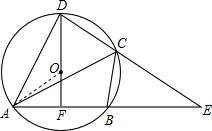
解：连接OA，
∵DF过点O，AF=FB=
，
∴∠AFO=90°．
∴FO=
=
=2．
∴DF=DO+FO=5．
∴AD=
=
．
DE=
=
．
由垂径定理知
=
，
∴∠DCA=∠DAB．
∵∠ADC是△ADC与△EDA的公共角，
∴△ADC∽△EDA．
∴
=
，
=
．
∴AC=
．
解：连接OA，∵DF过点O，AF=FB=
| 5 |
∴∠AFO=90°．
∴FO=
| AO2-AF2 |
| 9-5 |
∴DF=DO+FO=5．
∴AD=
| AF2+DF2 |
| 30 |
DE=
| FE2+DF2 |
| 70 |
由垂径定理知
 |
| AD |
|
| DB |
∴∠DCA=∠DAB．
∵∠ADC是△ADC与△EDA的公共角，
∴△ADC∽△EDA．
∴
| AC |
| AE |
| AD |
| DE |
| AC | ||
4
|
| ||
|
∴AC=
4
| ||
| 7 |
点评：本题主要考查了垂径定理、相似三角形的判定和性质、勾股定理等知识点，根据垂径定理得出角相等进而得出三角形相似是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
，
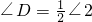．∵∠1+∠2=360°∴
，同理∠BAD+∠BCD=180°，即圆内接四边形对角（相对的两个角）互补．