题目内容
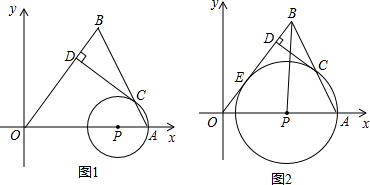
已知,点A(10,0)B(6,8),点P为线段OA上一动点(不与点A、点O重合),以PA为半径的⊙P与线段AB的另一个交点为C,作CD⊥OB于D(如图1)
(1)求证:CD是⊙P的切线;
(2)求当⊙P与OB相切时⊙P的半径;
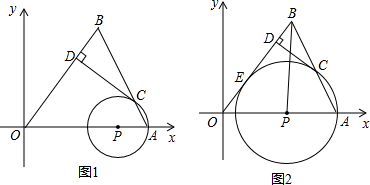
(3)在(2)的情况下,设(2)中⊙P与OB的切点为E,连接PB交CD于点F(如图2)
①求CF的长;
②在线段DE上是否存在点G使∠GPF=45°?若存在,求出EG的长;若不存在,请说明理由.

(1)求证:CD是⊙P的切线;
(2)求当⊙P与OB相切时⊙P的半径;
(3)在(2)的情况下,设(2)中⊙P与OB的切点为E,连接PB交CD于点F(如图2)
①求CF的长;
②在线段DE上是否存在点G使∠GPF=45°?若存在,求出EG的长;若不存在,请说明理由.
分析:(1)如图1,连接PC,过B作BN⊥x轴于点N.欲证CD是⊙P的切线,只需证明PC⊥CD即可;
(2)如图2,过B作BN⊥x轴于点N,设圆P的半径为r.根据切线的性质知PE⊥OE,所以在Rt△OPE和Rt△OBN中,利用∠BON的正弦函数的定义列出关于r的比例式
=
,由此可以求得r的值;
(3)①如图3,由正方形PCDE的四条边相等知DE=DC=r,则BD=OB-OE-DE.然后将其代入相似三角形(△BDF∽△PCF)的对应边成比例的比例式
=
中,从而求得CF的值;
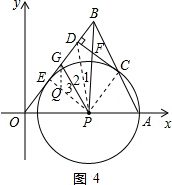
②假设在线段DE上是否存在点G使∠GPF=45°.如图4所示,在线段DE上截取EQ=EG.通过相似三角形:△GQP∽△BDP
,的对应边成比例求得BD=
,然后将相关线段的长度代入该比例式来求线段EG的长度.
(2)如图2,过B作BN⊥x轴于点N,设圆P的半径为r.根据切线的性质知PE⊥OE,所以在Rt△OPE和Rt△OBN中,利用∠BON的正弦函数的定义列出关于r的比例式
| r |
| 10-r |
| 4 |
| 5 |
(3)①如图3,由正方形PCDE的四条边相等知DE=DC=r,则BD=OB-OE-DE.然后将其代入相似三角形(△BDF∽△PCF)的对应边成比例的比例式
| BD |
| PC |
| DF |
| CF |
②假设在线段DE上是否存在点G使∠GPF=45°.如图4所示,在线段DE上截取EQ=EG.通过相似三角形:△GQP∽△BDP
,的对应边成比例求得BD=
| 20 |
| 9 |
解答: 解:(1)连接PC,过B作BN⊥x轴于点N.
解:(1)连接PC,过B作BN⊥x轴于点N.
∵PC=PA(⊙P的半径),
∴∠1=∠2(等边对等角).
∵A(10,0),B(6,8),
∴OA=10,BN=8,ON=6,
∴在Rt△OBN中,OB=
=10(勾股定理),
∴OA=OB,
∴∠OBA=∠1(等边对等角),
∴∠OBA=∠2(等量代换),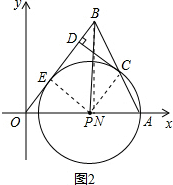
∴PC∥OB(同位角相等,两直线平行).
∵CD⊥OB,
∴CD⊥PC,
∴CD为⊙P的切线;
(2)如图2,过B作BN⊥x轴于点N,设圆P的半径为r.
∵⊙P与OB相切于点E,则OB⊥PE,OA=10,
∴在Rt△OPE中,sin∠EOP=
=
,
在Rt△OBN中,sin∠BON=
=
=
,
∴
=
,
解得:r=
;
(3)①如图3,∵由(2)知r=
,
∴在Rt△OPE中,OE=
=
=
(勾股定理),
∵∠PCD=∠CDE=∠PED=90°,
∴四边形PCDE是矩形.
又∵PE=PC(⊙O的半径),
∴矩形PCDE是正方形,
∴DE=DC=r=
,
∴BD=OB-OE-DE=10-
-
=
.
∵∠BFD=∠PFC,∠PEO=∠PCF=90°,
∴△BDF∽△PCF,
∴
=
,即
=
,
解得,CF=
,即CF的长度是
;
②假设在线段DE上是否存在点G使∠GPF=45°.
如图4所示,在线段DE上截取EQ=EG.
∵OB⊥PE,
∴∠GQE=45°,
∴∠GQP=135°.
∵四边形PCDE是正方形,
∴PD=
PC=
,∠EPD=∠PDC=45°,
∴∠2+∠3=45°.
∵∠FPG=45°,
∴∠1+∠2=45°
∴∠1=∠3
∵∠BDP=∠BDC+∠PDC=90°+45°=135°
∴∠GQP=∠BDP
∴△GQP∽△BDP
∴
=
∵OE=
,DE=
,OB=10,
∴BD=OB-ED-OE=
.
设EG=a,则GQ=
a,PQ=PE-EQ=
-a,
∴
=
,
解得,a=
,即EG的长度是
.
 解:(1)连接PC,过B作BN⊥x轴于点N.
解:(1)连接PC,过B作BN⊥x轴于点N.∵PC=PA(⊙P的半径),
∴∠1=∠2(等边对等角).
∵A(10,0),B(6,8),
∴OA=10,BN=8,ON=6,
∴在Rt△OBN中,OB=
| ON2+BN2 |
∴OA=OB,
∴∠OBA=∠1(等边对等角),
∴∠OBA=∠2(等量代换),

∴PC∥OB(同位角相等,两直线平行).
∵CD⊥OB,
∴CD⊥PC,
∴CD为⊙P的切线;
(2)如图2,过B作BN⊥x轴于点N,设圆P的半径为r.
∵⊙P与OB相切于点E,则OB⊥PE,OA=10,
∴在Rt△OPE中,sin∠EOP=
| PE |
| OP |
| r |
| 10-r |
在Rt△OBN中,sin∠BON=
| BN |
| OB |
| 8 |
| 10 |
| 4 |
| 5 |
∴
| r |
| 10-r |
| 4 |
| 5 |
解得:r=
| 40 |
| 9 |

(3)①如图3,∵由(2)知r=
| 40 |
| 9 |
∴在Rt△OPE中,OE=
| OP2-PE2 |
(10-
|
| 10 |
| 3 |
∵∠PCD=∠CDE=∠PED=90°,
∴四边形PCDE是矩形.
又∵PE=PC(⊙O的半径),
∴矩形PCDE是正方形,
∴DE=DC=r=
| 40 |
| 9 |

∴BD=OB-OE-DE=10-
| 10 |
| 3 |
| 40 |
| 9 |
| 20 |
| 9 |
∵∠BFD=∠PFC,∠PEO=∠PCF=90°,
∴△BDF∽△PCF,
∴
| BD |
| PC |
| DF |
| CF |
| ||
|
| ||
| CF |
解得,CF=
| 80 |
| 27 |
| 80 |
| 27 |
②假设在线段DE上是否存在点G使∠GPF=45°.
如图4所示,在线段DE上截取EQ=EG.
∵OB⊥PE,
∴∠GQE=45°,
∴∠GQP=135°.
∵四边形PCDE是正方形,
∴PD=
| 2 |
40
| ||
| 9 |
∴∠2+∠3=45°.
∵∠FPG=45°,
∴∠1+∠2=45°
∴∠1=∠3
∵∠BDP=∠BDC+∠PDC=90°+45°=135°
∴∠GQP=∠BDP
∴△GQP∽△BDP
∴
| GQ |
| BD |
| PQ |
| PD |
∵OE=
| 10 |
| 3 |
| 40 |
| 9 |
∴BD=OB-ED-OE=
| 20 |
| 9 |
设EG=a,则GQ=
| 2 |
| 40 |
| 9 |
∴
| ||
|
| ||||
|
解得,a=
| 8 |
| 9 |
| 8 |
| 9 |
点评:本题考查了圆的综合题.解题时,注意“数学结合”数学思想的应用.在证明(3)②时,巧妙的运用了旋转的性质,切线的性质求得EG的长度.

练习册系列答案
相关题目
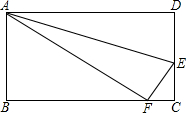 如图,将矩形ABCD沿AE折叠,使点D落在BC边上的F处,已知AB=6,BC=10,则EC=
如图,将矩形ABCD沿AE折叠,使点D落在BC边上的F处,已知AB=6,BC=10,则EC=