题目内容
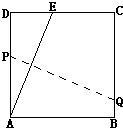12、如图，将一块边长为12的正方形纸片ABCD的顶点A折叠至DC边上的点E，使DE=5，折痕为PQ，则PQ的长为13
．分析：利用线段平移和全等三角形的性质．
解答：解：∵AD=12，DE=5，∠D=90°，
∴AE=13．
做BF∥PQ交AD于点F，易得四边形BFPQ是平行四边形，
那么PQ=BF，由折叠得到PQ⊥AE，
那么BF⊥AE，
∴∠FBA+∠EAB=90°．
∵∠DAE+∠EAB=90°，
∴∠ABF=∠DAE．
由正方形性质可得AD=AB，∠D=∠BAD=90°．
∴△ABF≌△DAE．
∴BF=AE=13．
则PQ=AR=13．
∴AE=13．
做BF∥PQ交AD于点F，易得四边形BFPQ是平行四边形，
那么PQ=BF，由折叠得到PQ⊥AE，
那么BF⊥AE，
∴∠FBA+∠EAB=90°．
∵∠DAE+∠EAB=90°，
∴∠ABF=∠DAE．
由正方形性质可得AD=AB，∠D=∠BAD=90°．
∴△ABF≌△DAE．
∴BF=AE=13．
则PQ=AR=13．
点评：所求线段应进行平移，构造相应的全等三角形求解．
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
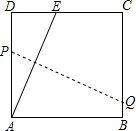如图，将一块边长为12的正方形纸片ABCD的顶点A折叠至DC边上的点E，使DE=5，折痕为PQ，则PQ的长为（ ）| A、12 | B、13 | C、14 | D、15 |
如图，将一块边长为4cm的正方形纸片ABCD，叠放在一块足够大的直角三角板上（并使直角顶点落在A点），设三角板的两直角边分别与CD交于点F，与CB延长线交于点E，那么四边形AECF的面积为（ ）
