题目内容
【题目】对x,y定义一种新运算T,规定:T(x,y)=ax+2by﹣1(其中a、b均为非零常数),这里等式右边是通常的四则运算,例如:T(0,1)=a0+2b1﹣1=2b﹣1.
(1)已知T(1,﹣1)=﹣2,T(4,2)=3.
①求a,b的值;
②若关于m的不等式组 恰好有2个整数解,求实数p的取值范围;
恰好有2个整数解,求实数p的取值范围;
(2)若T(x,y)=T(y,x)对任意实数x,y都成立(这里T(x,y)和T(y,x)均有意义),则a,b应满足怎样的关系式?
【答案】(1)①a=1,b=3;②-2≤p<-![]() ;(2)a=2b.
;(2)a=2b.
【解析】试题分析:(1)①已知两对值代入T中计算求出a与b的值;
②根据题中新定义化简已知不等式,根据不等式组恰好有3个整数解,求出p的范围即可;
(2)由T(x,y)=T(y,x)列出关系式,整理后即可确定出a与b的关系式.
试题解析:(1)①根据题意得:T(1,-1)=![]() =-2,即a-b=-2;
=-2,即a-b=-2;
T=(4,2)=![]() =1,即2a+b=5,
=1,即2a+b=5,
解得:a=1,b=3;
②根据题意得: 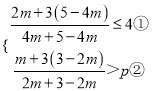 ,
,
由①得:m≥-![]() ;
;
由②得:m<![]() ,
,
∴不等式组的解集为-![]() ≤m<
≤m<![]() ,
,
∵不等式组恰好有3个整数解,即m=0,1,2,
∴2<![]() ≤3,
≤3,
解得:-2≤p<-![]() ;
;
(2)由T(x,y)=T(y,x),得到![]() =
=![]() ,
,
整理得:(x2-y2)(2b-a)=0,
∵T(x,y)=T(y,x)对任意实数x,y都成立,
∴2b-a=0,即a=2b.

 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案【题目】为降低空气污染,启东飞鹤公交公司决定全部更换节能环保的燃气公交车.计划购买A型和B型两种公交车共10辆,其中每台的价格,年载客量如表:
A型 | B型 | |
价格(万元/台) | a | b |
年载客量(万人/年) | 60 | 100 |
若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元.
(1)求a,b的值;
(2)如果该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客总和不少于680万人次.请你设计一个方案,使得购车总费用最少.