题目内容
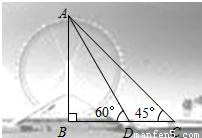
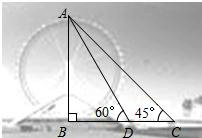 永乐桥摩天轮是天津市的标志性景观之一某校数学兴趣小组要测量摩天轮的高度如图,他们在C处测得摩天轮的最高点A的仰角为45°,再往摩天轮的方向前进50m至D处,测得最高点A的仰角为60°.求该兴趣小组测得的摩天轮的高度AB.(
永乐桥摩天轮是天津市的标志性景观之一某校数学兴趣小组要测量摩天轮的高度如图,他们在C处测得摩天轮的最高点A的仰角为45°,再往摩天轮的方向前进50m至D处,测得最高点A的仰角为60°.求该兴趣小组测得的摩天轮的高度AB.(| 3 |
分析:分别在Rt△ABD和Rt△ABC中,用AB表示出BC、BD的长,进而由CD=BC-BD=50求出AB的长.
解答:解:根据题意,可知∠ACB=45°,∠ADB=60°,DC=50.
在Rt△ABC中,
∵∠BAC=∠BCA=45°,
∴BC=AB.
在Rt△ABD中,tan∠ADB=
,
∴BD=
=
=
AB.
又∵BC-BD=DC,
∴AB-
AB=50,
即(3-
)AB=150,
∴AB=
=75+25
≈118m
答:该兴趣小组测得的摩天轮的高度约为118m.
在Rt△ABC中,
∵∠BAC=∠BCA=45°,
∴BC=AB.
在Rt△ABD中,tan∠ADB=
| AB |
| BD |
∴BD=
| AB |
| tan∠ADB |
| AB |
| tan60° |
| ||
| 3 |
又∵BC-BD=DC,
∴AB-
| ||
| 3 |
即(3-
| 3 |
∴AB=
| 150 | ||
3-
|
| 3 |
答:该兴趣小组测得的摩天轮的高度约为118m.
点评:此题的两个直角三角形拥有公共直角边,能够合理的运用这条公共边是解答此题的关键.

练习册系列答案
相关题目
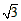 ≈1.732,结果保留整数)
≈1.732,结果保留整数)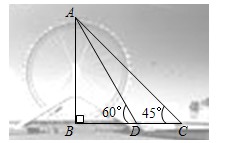
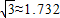 ,结果保留整数)
,结果保留整数)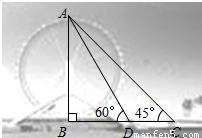
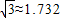 ,结果保留整数)
,结果保留整数)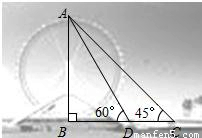
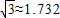 ,结果保留整数)
,结果保留整数)