题目内容
(1)探究下表中的奥秘,并完成填空:
(2)仿照上表把二次三项式 (其中
(其中 )进行分解?
)进行分解?
| 一元二次方程 | 根 | 二次三项式 |
 |  |  |
 |  |  |
 | ________________ |  |
 |  |  |
 | _________________ |  |
 (其中
(其中 )进行分解?
)进行分解?(1)
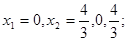
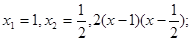
(2)

(1)考查了二次三项式为0时,方程的根与二次三项式的因式分解的关系,按照题目所给规律填空即可;
(2)利用配方法解方程ax2+bx+c=0,再根据规律把ax2+bx+c因式分解.
解:(1)
故本题答案为:x1=0,x2=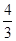 ,0,
,0,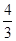 ;x1=1,x2=
;x1=1,x2=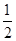 ,2(x-1)(x-
,2(x-1)(x-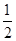 );
);
(2)方程ax2+bx+c=0,
移项,得ax2+bx=-c,
化系数为1,得x2+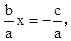
配方,得x2+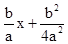 =-
=-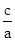 +
+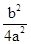 ,
,
(x+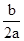 )2=
)2=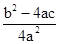 ,
,
解得,x1=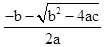 ,x2=
,x2=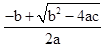 ,
,
∴ax2+bx+c=a(x-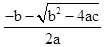 )(x-
)(x-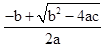 ).
).
(2)利用配方法解方程ax2+bx+c=0,再根据规律把ax2+bx+c因式分解.
解:(1)
| 一元二次方程 | 根 | 二次三项式 | ||||
| x2-25=0 | x1=5,x2=-5 | x2-25=(x-5)(x+5) | ||||
| x2+6x-16=0 | x1=2,x2=-8 | x2+6x-16=(x-2)(x+8) | ||||
| 3x2-4x=0 | x1=0,x2=
| 3x2-4x=3(x-0)(x-
| ||||
| 5x2-4x-1=0 | x1=5,x2=- | 5x2-4x-1=5(x-1)(x+) | ||||
| 2x2-3x+1=0 | x1=1,x2=
| 2x2-3x+1=2(x-1)(x-
|
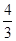 ,0,
,0,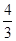 ;x1=1,x2=
;x1=1,x2=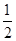 ,2(x-1)(x-
,2(x-1)(x-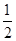 );
);(2)方程ax2+bx+c=0,
移项,得ax2+bx=-c,
化系数为1,得x2+
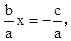
配方,得x2+
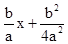 =-
=-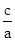 +
+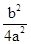 ,
,(x+
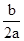 )2=
)2=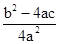 ,
,解得,x1=
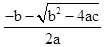 ,x2=
,x2=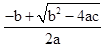 ,
,∴ax2+bx+c=a(x-
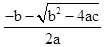 )(x-
)(x-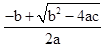 ).
).
练习册系列答案
相关题目
 的方程
的方程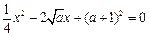 有实根.
有实根.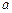 的值;
的值;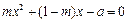 的所有根均为整数,求整数
的所有根均为整数,求整数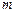 的值
的值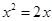 的根为( )
的根为( )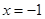 是关于
是关于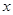 的方程
的方程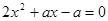 的一个根,则
的一个根,则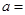 ____
____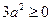 ,所以
,所以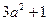 就有最小值1,即
就有最小值1,即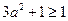 ,只有当
,只有当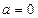 时,才能得到这个式子的最小值1.同样,因为
时,才能得到这个式子的最小值1.同样,因为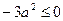 ,所以
,所以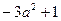 有最大值1,即
有最大值1,即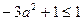 ,只有在
,只有在
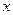 = 时,代数式
= 时,代数式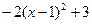 有最 (填写大或小)值为 .
有最 (填写大或小)值为 .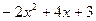 有最 (填写大或小)值为 .
有最 (填写大或小)值为 .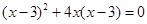 .(5分)
.(5分)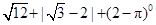 .(5分)
.(5分)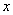 的一元二次方程的一个根是1,写出一个符合条件的方程:
的一元二次方程的一个根是1,写出一个符合条件的方程: 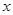 的方程
的方程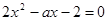 有两个相等的实数根,则
有两个相等的实数根,则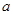 的值是( )
的值是( )