题目内容
如图，BE是△ABC的外接⊙O的直径，CD是△ABC的高．（1）求证：
| AC |
| BE |
| DC |
| BC |
（2）已知：AB=11，AD=3，CD=6，求⊙O的直径BE的长．
分析：（1）易得，∠BCE=∠ADC=90°，∠A=∠E，故有△ADC∽△ECB，∴CD：BC=AC：BE；
（2）由勾股定理求得AC，BC后，利用△ADC∽△ECB的性质求得BE的值．
（2）由勾股定理求得AC，BC后，利用△ADC∽△ECB的性质求得BE的值．
解答：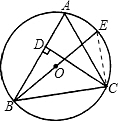
（1）证明：连接EC，
∵BE是直径，∴∠BCE=∠ADC=90°，
又∵∠A=∠E，∴△ADC∽△ECB，
∴CD：BC=AC：BE．
（2）解：由题意知，BD=11-3=8，
在Rt△ACD中，由勾股定理知，AC=
=3
，
在Rt△BCD中，由勾股定理知，BC=
=10，
由（1）知，CD：BC=AC：BE，
∴BE=
=5
．
（1）证明：连接EC，∵BE是直径，∴∠BCE=∠ADC=90°，
又∵∠A=∠E，∴△ADC∽△ECB，
∴CD：BC=AC：BE．
（2）解：由题意知，BD=11-3=8，
在Rt△ACD中，由勾股定理知，AC=
| AD2+CD2 |
| 5 |
在Rt△BCD中，由勾股定理知，BC=
| BD2+CD2 |
由（1）知，CD：BC=AC：BE，
∴BE=
| AC•BC |
| CD |
| 5 |
点评：本题利用了勾股定理，直径对的圆周角是直角，圆周角定理，相似三角形的判定和性质求解．
练习册系列答案
相关题目
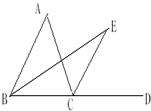19、如图，BE是∠ABC的角平分线，AB∥CE，如果已知∠A=50°，∠E=30°，则∠ACD=
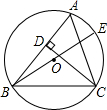已知：如图，BE是△ABC的外接圆O的直径，CD是△ABC的高．
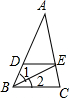如图，BE是△ABC中∠ABC的平分线．DE∥BC，若AE=3，AD=4，AC=5，求DE的长．
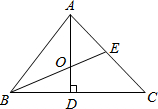如图，BE是△ABC的角平分线，AD是△ABC的高，∠ABC=60°，则∠AOE=