题目内容
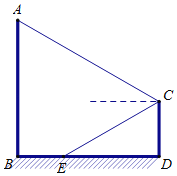
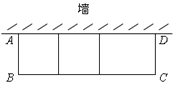
【题目】如图，用一段100米长的篱笆围成一个一边靠墙（墙足够长），中间用篱笆隔开的矩形养殖场，中间用两道篱笆隔开分出三个小的矩形，设矩形垂直于墙的一边长为x 米，矩形ABCD的面积记为y平方米．
（1）直接写出y与x的函数关系式及自变量x的取值范围；
（2）当x=8，求y的值；
（3）当x取何值时，y的值最大，最大值是多少？
【答案】（1）
,（0＜x＜25）；（2）544平方米；（3）y有最大值，最大值625平方米.
【解析】
（1）根据y=ABBC=x（100-4x）（0＜x＜25），求y与x之间的函数关系式即可；
（2）把x=8代入（1）中函数关系式求解即可；
（3）利用公式可求y的最大值及此时x的值．
（1）由题意，
（0＜x＜25）
（2）当x=8时，y=－4×82＋800
=544平方米
（3）x=
=12.5时，
y有最大值，最大值625平方米.
练习册系列答案
相关题目
【题目】某单位招聘员工两名，采取笔试与面试相结合的方式进行，两项成绩原始分满分均为100分，前六名选手的得分如下：
序号项目 | 1 | 2 | 3 | 4 | 5 | 6 |
笔试成绩（分） | 85 | 92 | 84 | 90 | 84 | 80 |
面试成绩（分） | 90 | 83 | 82 | 90 | 80 | 85 |
（1）这6名选手笔试成绩的中位数是________分，众数是________分．
（2）现得知1号选手的综合成绩为88分，求笔试成绩和面试成绩各占的百分比；
（3）在（2）的情况下________，（填序号）选手会被录取．
