题目内容
在△ABC中,若
+|
-cosC|=0,且∠B,∠C都是锐角,则∠A的度数是( )
sinB-
|
| 1 |
| 2 |
| A、15° | B、60° |
| C、75° | D、30° |
分析:先根据非负数的性质求出sinB及cosC的值,再由特殊角的三角函数值解答即可.
解答:解:∵
+|
-cosC|=0,
∴sinB-
=0;
-cosC=0.
即sinB=
;cosC=
.
∴∠B=45°,∠C=60°.
∴∠A=180°-∠B-∠C=180°-45°-60°=75°.
故选C.
sinB-
|
| 1 |
| 2 |
∴sinB-
| ||
| 2 |
| 1 |
| 2 |
即sinB=
| ||
| 2 |
| 1 |
| 2 |
∴∠B=45°,∠C=60°.
∴∠A=180°-∠B-∠C=180°-45°-60°=75°.
故选C.
点评:此题涉及到非负数的性质、特殊角的三角函数值及三角形内角和定理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在△ABC中,若|sinB-
|与(
-cosA)2互为相反数,则∠C等于( )
| 1 |
| 2 |
| ||
| 2 |
| A、120° | B、90° |
| C、60° | D、45° |
 |与(
|与(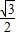 -cosA)2互为相反数,则∠C等于( )
-cosA)2互为相反数,则∠C等于( ) |与(
|与( -cosA)2互为相反数,则∠C等于( )
-cosA)2互为相反数,则∠C等于( )