题目内容
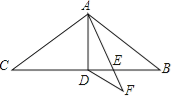
【题目】如图，一次函数y=kx+b的图象与反比例函数y= 
（x＞0）的图象交于A（2，﹣1），B（ 
，n）两点，直线y=2与y轴交于点C．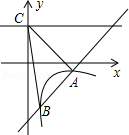 
（1）求一次函数与反比例函数的解析式；
（2）求△ABC的面积．
【答案】
（1）解：把A（2，﹣1）代入反比例解析式得：﹣1= 
，即m=﹣2，
∴反比例解析式为y=﹣ 
，
把B（ 
，n）代入反比例解析式得：n=﹣4，即B（ ，﹣4），
把A与B坐标代入y=kx+b中得：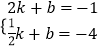 
，
解得：k=2，b=﹣5，
则一次函数解析式为y=2x﹣5；
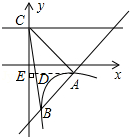
（2）解：∵A（2，﹣1），B（ ，﹣4），直线AB解析式为y=2x﹣5，
∵C（0，2），直线BC解析式为y=﹣12x+2，
将y=﹣1代入BC的解析式得x= 
，则AD=2﹣ = 
．
∵xC﹣xB=2﹣（﹣4）=6，
∴S△ABC= ×AD×（yC﹣yB）= × ×6= 
．
【解析】（1）把A坐标代入反比例解析式求出m的值，确定出反比例解析式，再将B坐标代入求出n的值，确定出B坐标，将A与B坐标代入一次函数解析式求出k与b的值，即可确定出一次函数解析式；（2）利用两点间的距离公式求出AB的长，利用点到直线的距离公式求出点C到直线AB的距离，即可确定出三角形ABC面积．
阅读快车系列答案【题目】如图，广宇购物中心设立了一个可以自由转动的转盘，并规定：顾客购物满20元以上就能获得一次转动转盘的机会，当转盘停止时，指针落在哪一区域就可以获得相应的奖品，下表是活动进行中的一组统计数据．
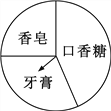
转动转盘的次数n | 100 | 200 | 400 | 500 | 1000 |
落在“牙膏”区域的次数m | 32 | 58 | 121 | 149 | 300 |
落在“牙膏”区域的频率 | 0.3025 |
(1)计算并完成上面的表格；
(2)请估计，当n很大时，频率将会接近多少？
(3)假如你去转动该转盘一次，你获得牙膏的概率是多少？
