题目内容
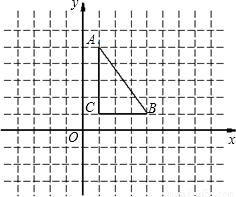
如图△ABC三点的坐标为A(1,4),B(5,1),C(1,1).
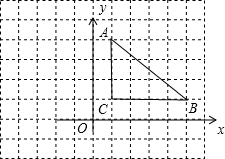
①作出△ABC关于y轴对称得到的△A1B1C1,则B1坐标为________;
②作出△ABC绕点C逆时针旋转90得到的△A2B2C2,则A2的坐标为________;
③△A1B1C1与△A2B2C2重叠部分的面积是________.
(-5,1) (-2,1) 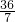
分析:(1)B1与B关于y轴对称,故纵坐标不变,横坐标互为相反数.
(2)将线段CA绕C旋转90°即可得到对应线段C2A2,从而求出A2的坐标.
(3)由图象变换的性质,分别作出△A1B1C1与△A2B2C2,可得到其重叠部分为轴对称图形,故分成全等的两个三角形求解.
解答:(1)B1与B关于y轴对称,故B1坐标为(-1,4).
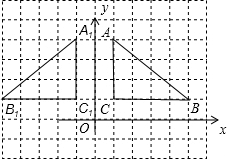
(2)将△ABC绕点C逆时针旋转90得到△A2B2C2,其图象为:
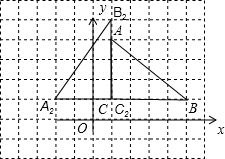
则A2的坐标为(-2,1).
(3)
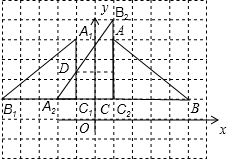 .
.
△A1B1C1与△A2B2C2重叠部分可有DC分成全等的两个三角形,设它们的高为h,
则△A2B2C2的面积为 ×3×h+
×3×h+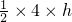 =
=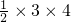 ,解得h=
,解得h= ,
,
故重叠部分的面积是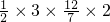 =
=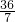 .
.
点评:本题考查旋转变换作图和轴对称作图,关键要掌握各种变换的特点,在求重叠部分的面积时,运用了方程思想.
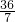
分析:(1)B1与B关于y轴对称,故纵坐标不变,横坐标互为相反数.
(2)将线段CA绕C旋转90°即可得到对应线段C2A2,从而求出A2的坐标.
(3)由图象变换的性质,分别作出△A1B1C1与△A2B2C2,可得到其重叠部分为轴对称图形,故分成全等的两个三角形求解.
解答:(1)B1与B关于y轴对称,故B1坐标为(-1,4).

(2)将△ABC绕点C逆时针旋转90得到△A2B2C2,其图象为:

则A2的坐标为(-2,1).
(3)
 .
.△A1B1C1与△A2B2C2重叠部分可有DC分成全等的两个三角形,设它们的高为h,
则△A2B2C2的面积为
 ×3×h+
×3×h+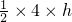 =
=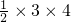 ,解得h=
,解得h= ,
,故重叠部分的面积是
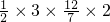 =
=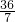 .
.点评:本题考查旋转变换作图和轴对称作图,关键要掌握各种变换的特点,在求重叠部分的面积时,运用了方程思想.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
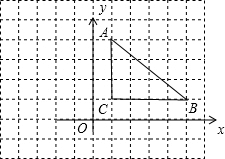
 如图△ABC三点的坐标分别为A(1,5),B(4,1),C(1,1)
如图△ABC三点的坐标分别为A(1,5),B(4,1),C(1,1)