Question

【题目】（阅读）

辅助线是几何解题中沟通条件与结论的桥梁．在众多类型的辅助线中，辅助圆作为一条曲线型辅助线，显得独特而隐蔽．

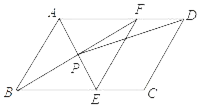
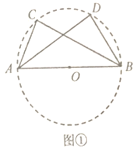
性质：如图①，若，则点在经过，，三点的圆上．

（问题解决）

运用上述材料中的信息解决以下问题：

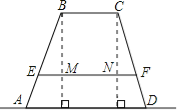
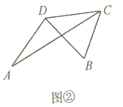
（1）如图②，已知．求证：．

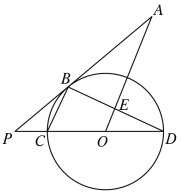
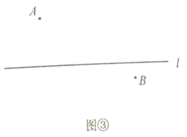
（2）如图③，点，位于直线两侧．用尺规在直线上作出点，使得．（要求：要有画图痕迹，不用写画法）

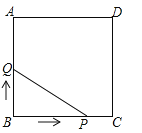
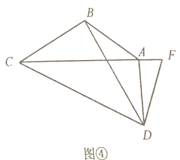
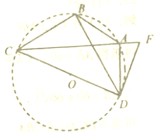
（3）如图④，在四边形中，，，点在的延长线上，连接，．求证：是外接圆的切线．

Answer 1

【答案】（1）见解析；（2）见解析；（3）见解析

【解析】

(1)作以为圆心，为半径的圆,根据圆周角性质可得;(2) 作以AB中点P为圆心，为半径的圆,根据圆周角定理可得；（3）取的中点，则是的外接圆．由，可得点在的外接圆上．根据切线判定定理求解.

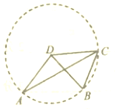
（1）如图，由，可知:

点，，在以为圆心，为半径的圆上．

所以，．

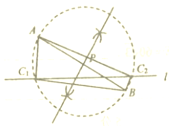
（2）如图，点，就是所要求作的点．

（3）如图，取的中点，则是的外接圆．

由，可得点在的外接圆上．

∴．

∵，

∴．

∵，

∴．

∴．

即．

∴是外接圆的切线．