题目内容
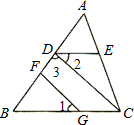
19、计算：如图所示，DE∥BC，CD∥GF，且∠1=40°，∠B=35°．求∠2和∠3的度数．分析：由∠1=40°，∠B=35°，根据三角形内角和定理，即可求得∠GFB的度数，又由DE∥BC，CD∥GF，根据两直线平行内错角相等与两直线平行，同位角相等，即可求得∠2和∠3的度数．
解答：解：∵∠1=40°，∠B=35°，
∴∠GFB=105°，
∵CD∥GF，
∴∠DCB=∠1=40°，∠3=∠GFB=105°，
∵DE∥BC，
∴∠2=∠DCB=40°．
∴∠2=40°，∠3=105°．
∴∠GFB=105°，
∵CD∥GF，
∴∠DCB=∠1=40°，∠3=∠GFB=105°，
∵DE∥BC，
∴∠2=∠DCB=40°．
∴∠2=40°，∠3=105°．
点评：此题考查了平行线的性质与三角形内角定理．此题比较简单，注意掌握两直线平行内错角相等与两直线平行，同位角相等定理的应用，注意数形结合思想的应用．
练习册系列答案
名校课堂系列答案
相关题目
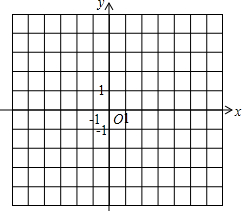已知五点A、B、C、DE的坐标分别是（-2，0）、（2，-3）、（3，-1）、（3，1）、（2，3）
