题目内容
(2004•广州)如图,直线y= (x+1)分别与x轴、y轴相交于A、B两点,等边△ABC的顶点C在第二象限.
(x+1)分别与x轴、y轴相交于A、B两点,等边△ABC的顶点C在第二象限.(1)在所给图中,按尺规作图要求,求作等边△ABC(保留作图痕迹,不写作法);
(2)若一次函数y=kx+b的图象经过A、C两点,求k、b的值;
(3)以坐标原点O为圆心、OB的长为半径的圆交线段CA于点D,交CA的延长线于点E.求证:BD⊥CE.

【答案】分析:(1)在所给图中,按尺规作图要求,求作等边△ABC,三角形的顶点C,应该在线段AB的垂直平分线上,并且到A得距离是AB的长;
(2)根据等边三角形的性质可以求出C点的坐标,A点的坐标,根据待定系数法就可以求出函数解析式,得到k,b的值;
(3)只要证明BE是圆的直径就可以.
解答: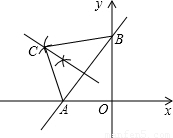 (1)解:图如右,
(1)解:图如右,
(2)解:在直线y=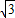 (x+1)中令x=0,y=0分别解得y=
(x+1)中令x=0,y=0分别解得y=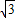 ,x=-1,
,x=-1,
因而A,B的坐标分别是(-1,0),(0, ),
),
则tan∠BAO=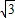 ,
,
∴∠BAO=60°,△ABC是等边三角形,
∴过点C作CD⊥x轴与D,则∠CAD=60°,CD= ,AD=1,因而C的坐标(-2,
,AD=1,因而C的坐标(-2,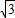 )
)
根据题意得到 ,解得
,解得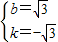 ;
;
(3)证明:直线AC的解析式是y=-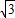 x-
x-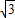 ,
,
在这个函数中令x=0,解得y=-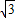 ,
,
则OB=OE,即BE是圆的直径,因而BD⊥CE.
点评:本题考查了待定系数法求函数解析式,以及圆周角的性质,直径所对的圆周角是直角.
(2)根据等边三角形的性质可以求出C点的坐标,A点的坐标,根据待定系数法就可以求出函数解析式,得到k,b的值;
(3)只要证明BE是圆的直径就可以.
解答:
 (1)解:图如右,
(1)解:图如右,(2)解:在直线y=
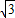 (x+1)中令x=0,y=0分别解得y=
(x+1)中令x=0,y=0分别解得y=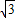 ,x=-1,
,x=-1,因而A,B的坐标分别是(-1,0),(0,
 ),
),则tan∠BAO=
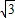 ,
,∴∠BAO=60°,△ABC是等边三角形,
∴过点C作CD⊥x轴与D,则∠CAD=60°,CD=
 ,AD=1,因而C的坐标(-2,
,AD=1,因而C的坐标(-2,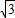 )
)根据题意得到
 ,解得
,解得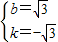 ;
;(3)证明:直线AC的解析式是y=-
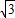 x-
x-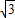 ,
,在这个函数中令x=0,解得y=-
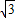 ,
,则OB=OE,即BE是圆的直径,因而BD⊥CE.
点评:本题考查了待定系数法求函数解析式,以及圆周角的性质,直径所对的圆周角是直角.

练习册系列答案
 同步奥数系列答案
同步奥数系列答案
相关题目
 (x+1)分别与x轴、y轴相交于A、B两点,等边△ABC的顶点C在第二象限.
(x+1)分别与x轴、y轴相交于A、B两点,等边△ABC的顶点C在第二象限.
 (2004•广州)如图,正六边形的螺帽的边长a=17mm,这个扳手的开口b最小应是多少?(结果精确到1mm)
(2004•广州)如图,正六边形的螺帽的边长a=17mm,这个扳手的开口b最小应是多少?(结果精确到1mm)
