题目内容
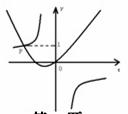
 运用图象法解答:如图,已知函数y=-
运用图象法解答:如图,已知函数y=-| 3 |
| x |
(-3,1)
(-3,1)
;②则关于x的方程ax2+bx+| 3 |
| x |
x<-3或x>0
x<-3或x>0
.分析:先根据点P的纵坐标为1求出x的值,再把于x的方程ax2+bx+
=0化为于x的方程ax2+bx=-
=0的形式,此方程就化为求函数y=-
与y=ax2+bx(a>0,b>0)的图象交点的横坐标,由求出的P点坐标,进而利用函数图象得出ax2+bx+
>0的解.
| 3 |
| x |
| 3 |
| x |
| 3 |
| x |
| 3 |
| x |
解答:解:∵P的纵坐标为1,
∴1=-
,
∴x=-3,
∵ax2+bx+
=0化为于x的方程ax2+bx=-
的形式,
∴此方程的解即为两函数图象交点的横坐标的值,
∴x=-3.
∴①两函数图象的交点为:(-3,1),
关于x的方程ax2+bx+
>0时,
即y=ax2+bx>y=-
时,结合图象即可得出:
x<-3或x>0,
故答案为:(-3,1);x<-3或x>0.
∴1=-
| 3 |
| x |
∴x=-3,
∵ax2+bx+
| 3 |
| x |
| 3 |
| x |
∴此方程的解即为两函数图象交点的横坐标的值,
∴x=-3.
∴①两函数图象的交点为:(-3,1),
关于x的方程ax2+bx+
| 3 |
| x |
即y=ax2+bx>y=-
| 3 |
| x |
x<-3或x>0,
故答案为:(-3,1);x<-3或x>0.
点评:本题考查的是二次函数的图象与反比例函数图象的交点问题,能把方程的解化为两函数图象的交点问题是解答此题的关键.

练习册系列答案
相关题目
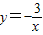 与y=ax2+bx(a>0,b>0)的图象交于点P,点P的纵坐标为1,则结论:①两函数图象的交点 ;②则关于x的方程ax2+bx
与y=ax2+bx(a>0,b>0)的图象交于点P,点P的纵坐标为1,则结论:①两函数图象的交点 ;②则关于x的方程ax2+bx >0的解为 .
>0的解为 .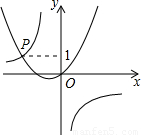
 与y=ax2+bx(a>0,b>0)的图象交于点P,点P的纵坐标为1,则结论:①两函数图象的交点 ;②则关于x的方程ax2+bx
与y=ax2+bx(a>0,b>0)的图象交于点P,点P的纵坐标为1,则结论:①两函数图象的交点 ;②则关于x的方程ax2+bx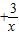 >0的解为 .
>0的解为 .
 与y=ax2+bx(a>0,b>0)的图象交于点P,点P的纵坐标为1,则结论:①两函数图象的交点 ;②则关于x的方程ax2+bx
与y=ax2+bx(a>0,b>0)的图象交于点P,点P的纵坐标为1,则结论:①两函数图象的交点 ;②则关于x的方程ax2+bx >0的解为 .
>0的解为 .