Question

【题目】已知三元一次方程组 ．
（1）求该方程组的解；
（2）若该方程组的解使ax+2y+z＜0成立，求整数a的最大值．

Answer 1

【答案】【解答】解：

①﹣②得：y﹣z=6④，
③与④组成二元一次方程组，
解得：；
把y=3代入①，解得x=2，
所以三元一次方程组的解为；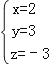
（2）∵该方程组的解使ax+2y+z＜0成立，
∴2a+6﹣3＜0，
∴a＜，
∴整数a的最大值为﹣2．
【解析】（1）根据解三元一次方程组的步骤先消去一个未知数，得到一个二元一次方程组，从而得出答案；
（2）将（1）中所求的方程组的解代入ax+2y+z＜0，求出a的取值范围，进而得到整数a的最大值．
【考点精析】通过灵活运用二元一次方程的解，掌握适合一个二元一次方程的一组未知数的值，叫做这个二元一次方程的一个解即可以解答此题．