题目内容
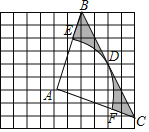
【题目】在如图所示的网格中,每个小正方形的边长为1,每个小正方形的顶点叫做格点.三角形ABC的三个顶点均在格点上,以点A为圆心的弧EF与BC相切于格点D,分别交AB,AC于点E,F.
(1)直接写出三角形ABC边长AB= ;AC= ;BC= .
(2)求图中由线段EB,BC,CF及弧FE所围成的阴影部分的面积.(结果保留π)
【答案】(1)2![]() ,2
,2![]() ,4
,4![]() ;(2)20﹣5π
;(2)20﹣5π
【解析】
(1)用勾股定理进行确定即可;
(3)用勾股定理逆定理确定该三角形为直角三角形,然后运用弧长公式求解即可;根据阴影部分的面积为S△ABC﹣S扇形AEF进行计算即可.
解:(1)AB=![]() =2
=2![]() ,
,
AC=![]() =2
=2![]() ,
,
BC=![]() =4
=4![]() ;
;
故答案为:2![]() ,2
,2![]() ,4
,4![]() ;
;
(2)由(1)得,AB2+AC2=BC2,
∴∠BAC=90°,
连接AD,AD=![]() =2
=2![]() ,
,
∴S阴=S△ABC﹣S扇形AEF=![]() ABAC﹣
ABAC﹣![]() πAD2=20﹣5π.
πAD2=20﹣5π.

练习册系列答案
相关题目