题目内容
升国旗时，某同学站在离旗杆底部24米处行注目礼，当国旗升至旗杆顶端时，该同学视线的仰角恰为30°，若双眼离地面1.5米，则旗杆的高度为
8
+1.5
| 3 |
8
+1.5
米．（用含根号的式子表示）| 3 |
分析：运用勾股定理的知识，即可得BC．由题意得BE=BC+CE，CE=AD，从而得出结果．
解答：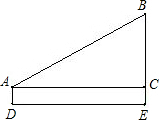
解：∵∠ACB=90°，∠BAC=30°，
∴AB=2BC，
设BC=x米，则AB=2x米，
∴在直角三角形ABC中，又DE=AC=24米，
根据勾股定理得：242+x2=（2x）2，
解得：x=8
即BC=8
∵BE=BC+CE，
∴BE=8
+1.5，
故答案为：8
+1.5．
解：∵∠ACB=90°，∠BAC=30°，∴AB=2BC，
设BC=x米，则AB=2x米，
∴在直角三角形ABC中，又DE=AC=24米，
根据勾股定理得：242+x2=（2x）2，
解得：x=8
| 3 |
即BC=8
| 3 |
∵BE=BC+CE，
∴BE=8
| 3 |
故答案为：8
| 3 |
点评：本题考查了解直角三角形的应用，解题的关键是从实际问题中整理出直角三角形并选择合适的边角关系解题，要求学生熟练掌握．
练习册系列答案
阳光试卷单元测试卷系列答案
相关题目
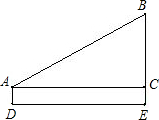升国旗时，某同学站在离旗杆底部（DE）24米处行注目礼，当国旗升至旗杆顶端B时，该同学视线的仰角（∠BAC）恰为30°，若双眼离地面（AD）1.5米，则旗杆的高度为（ ）米．| A、13、5 | ||
B、12
| ||
C、8
| ||
D、24
|