题目内容
 如图,在⊙O中,AB是直径,半径为R,
如图,在⊙O中,AB是直径,半径为R,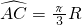 .
.
求:(1)∠AOC的度数;
(2)若D为劣弧BC上的一动点,且弦AD与半径OC交于E点.试探求△AEC≌△DEO时,D点的位置.
解:(1)∵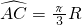 ,半圆的长是πR,
,半圆的长是πR,
∴弧AC是半圆是 ,即弧的度数是60°,
,即弧的度数是60°,
∴∠AOC=60°;
(2)D的位置,只要满足∠DOB=60°,或AC∥OD或劣弧BC的中点.
分析:(1)根据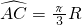 和半圆的长是πR,则弧AC是半圆是
和半圆的长是πR,则弧AC是半圆是 ,即弧的度数是60度,进而求得弧所对的圆心角的度数;
,即弧的度数是60度,进而求得弧所对的圆心角的度数;
(2)根据全等三角形的性质得到对应角相等,再根据内错角相等,两条直线平行,即可得到AC∥OD,或者结合(1)的结论发现等边三角形AOC,从而证明点D应是弧BC的中点.
点评:此题要能够根据弧的度数求得它所对的圆心角的度数.
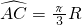 ,半圆的长是πR,
,半圆的长是πR,∴弧AC是半圆是
 ,即弧的度数是60°,
,即弧的度数是60°,∴∠AOC=60°;
(2)D的位置,只要满足∠DOB=60°,或AC∥OD或劣弧BC的中点.
分析:(1)根据
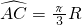 和半圆的长是πR,则弧AC是半圆是
和半圆的长是πR,则弧AC是半圆是 ,即弧的度数是60度,进而求得弧所对的圆心角的度数;
,即弧的度数是60度,进而求得弧所对的圆心角的度数;(2)根据全等三角形的性质得到对应角相等,再根据内错角相等,两条直线平行,即可得到AC∥OD,或者结合(1)的结论发现等边三角形AOC,从而证明点D应是弧BC的中点.
点评:此题要能够根据弧的度数求得它所对的圆心角的度数.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 如图,在△ABC中,AB>AC,E为BC边的中点,AD为∠BAC的平分线,过E作AD的平行线,交AB于F,交CA的延长线于G.
如图,在△ABC中,AB>AC,E为BC边的中点,AD为∠BAC的平分线,过E作AD的平行线,交AB于F,交CA的延长线于G. 如图,在△ABC中,AB=AC,D为BC边上一点,且∠BAD=30°,若AD=DE,∠EDC=33°,则∠DAE的度数为
如图,在△ABC中,AB=AC,D为BC边上一点,且∠BAD=30°,若AD=DE,∠EDC=33°,则∠DAE的度数为 如图,在△ABC中,AB=AC,D是△ABC内一点,且BD=DC.求证:∠ABD=∠ACD.
如图,在△ABC中,AB=AC,D是△ABC内一点,且BD=DC.求证:∠ABD=∠ACD.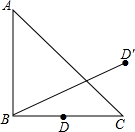 如图,在△ABC中,AB=BC,∠ABC=90°,D是BC的中点,且它关于AC的对称点是D′,BD′=
如图,在△ABC中,AB=BC,∠ABC=90°,D是BC的中点,且它关于AC的对称点是D′,BD′= 如图,在△ABC中,AB=AC,D点是BC的中点,DE⊥AB于E点,DF⊥AC于F点,则图中全等三角形共有
如图,在△ABC中,AB=AC,D点是BC的中点,DE⊥AB于E点,DF⊥AC于F点,则图中全等三角形共有