题目内容
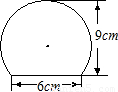
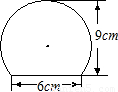
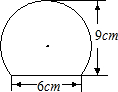如图是一个弓形零件的截面图．已知弓形高为9cm，弦长为6cm，求弓形所在圆的半径．分析：连接OA，过点O作OE⊥AB于点E，由垂径定理可知AE=
AB，设弓形所在圆的半径OA=r，则OE=9-r，在Rt△AOE中利用勾股定理即可得出r的值．
| 1 |
| 2 |
解答：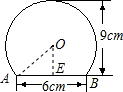
解：连接OA，过点O作OE⊥AB于点E，
∵OE⊥AB，AB=6cm，
∴AE=3cm，
设弓形所在圆的半径OA=r，则OE=9-r，
在Rt△AOE中，OA2=OE2+AE2，即r2=（9-r）2+32，
解得r=5cm．
故弓形所在圆的半径为5cm．
解：连接OA，过点O作OE⊥AB于点E，∵OE⊥AB，AB=6cm，
∴AE=3cm，
设弓形所在圆的半径OA=r，则OE=9-r，
在Rt△AOE中，OA2=OE2+AE2，即r2=（9-r）2+32，
解得r=5cm．
故弓形所在圆的半径为5cm．
点评：本题考查的是垂径定理的应用及勾股定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．
练习册系列答案
相关题目
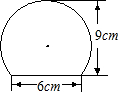如图是一个弓形零件的截面图．已知弓形高为9cm，弦长为6cm，求弓形所在圆的半径．
