题目内容
(9分)如下数表是由从1开始的连续自然数组成,观察规律并完成各题的解答.
1
2 3 4
5 6 7 8 9
10 11 12 13 14 15 16
17 18 19 20 21 22 23 24 25
26 27 28 29 30 31 32 33 34 35 36
…………………………
(1)表中第8行的最后一个数是______________,它是自然数_____________的平方,第8行共有____________个数;
(2)用含n的代数式表示:第n行的第一个数是______________,最后一个数是
________________,第n行共有_______________个数;
(3)求第50行各数之和.
1
2 3 4
5 6 7 8 9
10 11 12 13 14 15 16
17 18 19 20 21 22 23 24 25
26 27 28 29 30 31 32 33 34 35 36
…………………………
(1)表中第8行的最后一个数是______________,它是自然数_____________的平方,第8行共有____________个数;
(2)用含n的代数式表示:第n行的第一个数是______________,最后一个数是
________________,第n行共有_______________个数;
(3)求第50行各数之和.
(1)64,8,15;-------------------3分
(2)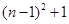 ,
, ,
,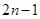 ;-------------------------6分
;-------------------------6分
(3)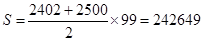 .-------------------9分
.-------------------9分
(2)
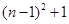 ,
, ,
,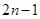 ;-------------------------6分
;-------------------------6分(3)
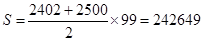 .-------------------9分
.-------------------9分分析:
(1)先从给的数中得出每行最后一个数是该行数的平方,即可求出第8行的最后一个数,再根据每行数的个数为1,3,5,…的奇数列,即可求出第8行共有的个数;
(2)根据第n行最后一数为n2,得出第一个数为n2-2n+2,根据每行数的个数为1,3,5,…的奇数列,即可得出答案;
(3)通过(2)得出的第n行的第一个数和最后一个数以及第n行共有的个数,列出算式,进行计算即可。
解答:
(1)从给的数中可得,每行最后一个数是该行数的平方,
则第8行的最后一个数是82=64,每行数的个数为1,3,5,…的奇数列,
第8行共有8×2-1=15个数;
故答案为:64,8,15;
(2)由(1)知第n行的最后一数为n2,
则第一个数为:(n-1)2+1=n2-2n+2,
第n行共有2n-1个数;
故答案为:(n-1)2+1,n2,2n-1;
(3)因为第n行的第一个数是(n-1)2+1,最后一个数是n2,共有(2n-1)个数,
所以第n行各数之和是[(n-1)2+1+n2]/2×(2n-1),
则第50行各数之和是[(50-1)2+1+502]/2×(2×50-1)=242649。
点评:本题考查了数字的变化类,通过观察,分析、归纳并发现其中的规律,并应用发现的规律解决问题是本题的关键。

练习册系列答案
相关题目
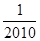
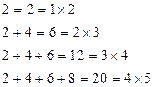
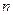 个连续偶数相加,和是多少?
个连续偶数相加,和是多少?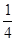 -│-22-4│-(-1
-│-22-4│-(-1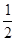 )3×
)3×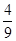 ;
; 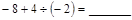 ,(2)
,(2) 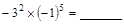 .
.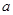 是最小的正整数,
是最小的正整数,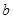 是最大的负整数,
是最大的负整数,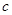 是绝对值最小的有理数,那么
是绝对值最小的有理数,那么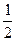 ,
,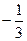 ,
, ,
, ,
,