题目内容
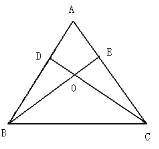
【题目】已知:如图,锐角△ABC的两条高BE、CD相交于点O,且OB=OC,
(1)求证:△ABC是等腰三角形;
(2)判断点O是否在∠BAC的角平分线上,并说明理由。
【答案】(1)、证明过程见解析;(2)、理由见解析
【解析】
试题分析:(1)、根据等腰三角形的性质以及高线得出△BDC和△CEB全等,从而得出∠DBC=∠ECB,得到等腰三角形;(2)、连接AO,根据△BDC和△CEB全等得到DC=EB,然后根据OB=OC得出OD=OE,结合∠BDC=∠CEB=90°和AO为公共边得出△ADO和△AEO全等从而得到答案.
试题解析:(1)、∵OB=OC ∴∠OBC=∠OCB ∵BE、CD是两条高 ∴∠BDC=∠CEB=90°
又∵BC=CB ∴△BDC≌△CEB(AAS) ∴∠DBC=∠ECB ∴AB=AC ∴△ABC是等腰三角形。
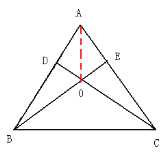
(2)、点O是在∠BAC的角平分线上。连结AO. ∵ △BDC≌△CEB ∴DC=EB,
∵OB=OC ∴ OD=OE 又∵∠BDC=∠CEB=90° AO=AO ∴△ADO≌△AEO(HL)
∴∠DAO=∠EAO ∴点O是在∠BAC的角平分线上。

练习册系列答案
相关题目