Question

18、已知△ABC，利用直尺和圆规，根据下列要求作图（保留作图痕迹，不要求写作法），并根据要求填空：
（1）作∠ABC的平分线BD交AC于点D；
（2）作线段BD的垂直平分线交AB于点E，交BC于点F．
（3）连接ED、FD，判断四边形BEDF是什么四边形．

Answer 1

分析：（1）以点B为圆心，任意长为半径画弧与AB，BC交于两点，再以这两点为圆心，大于两点间距离的一半为半径画弧，连接两弧的交点与B，与AC交于点D．BD就是所求的角平分线．
（2）分别以B、D为圆心，大于BD的一半为半径画弧，连接两弧的交点，交AB于点E，交BC与点F，EF就是所求的线段的垂直平分线；
（3）因为EF垂直平分BD，可求证△BOE≌△DOE、△BOF≌△DOF，又因为BD平分∠ABC，所以可证明ED∥BF、DF∥BE，
BE=DE，故四边形BEDF是菱形．

解答：解：从图中可能看出BD平分∠ABC，EF垂直平分BD；

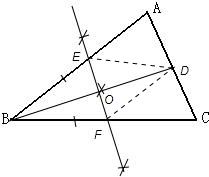
（3）平行四边形，如上图：
∵EF垂直平分BD
∴OB=OD，∠BOE=∠DOE
∵OE=OE
∴△BOE≌△DOE
∴∠EBO=∠EDO，BE=DE
∵∠EBO=∠FBO
∴∠EDO=∠FBO
∴ED∥BF
同理可证DF∥BE
∴四边形BEDF是菱形．

点评：本题主要考查了平行四边形的判定、线段垂直平分线的性质和角平分线的性质．两组对边分别平行的四边形是平行四边形．