题目内容
 如图,在Rt△ABC中,∠ABC=90°,点O为AC中点,点E为线段BC上一点,∠EOF=90°,OF交AB于点F,试给出线段AF、FE、EC之间的数量关系并证明.
如图,在Rt△ABC中,∠ABC=90°,点O为AC中点,点E为线段BC上一点,∠EOF=90°,OF交AB于点F,试给出线段AF、FE、EC之间的数量关系并证明.考点:全等三角形的判定与性质,等腰直角三角形
专题:几何图形问题,证明题,数形结合
分析:延长FO到M,使FO=OM,连接CM,EM,证△AOF≌△COM,推出AF=CM,∠A=∠MCO,求出∠MCE=90°,根据线段垂直平分线得出EF=EM,在Rt△MCE中,由勾股定理得出ME2=CM2+CE2,代入求出即可.
解答:证明: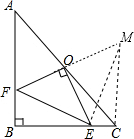
延长FO到M,使FO=OM,连接CM,EM,
∵点O是AC的中点,
∴OA=OC,
在△AOF和△COM中,
,
∴△AOF≌△COM(SAS),
∴AF=CM,∠A=∠MCO,
∴AB∥CM,
∵∠B=90°,
∴∠MCE=90°,
∵∠EOF=90°,OF=OM,
∴EF=EM,
在Rt△MCE中,由勾股定理得:ME2=CM2+CE2,
∵EF=EM,CM=AF,
∴AF2+CE2=EF2.

延长FO到M,使FO=OM,连接CM,EM,
∵点O是AC的中点,
∴OA=OC,
在△AOF和△COM中,
|
∴△AOF≌△COM(SAS),
∴AF=CM,∠A=∠MCO,
∴AB∥CM,
∵∠B=90°,
∴∠MCE=90°,
∵∠EOF=90°,OF=OM,
∴EF=EM,
在Rt△MCE中,由勾股定理得:ME2=CM2+CE2,
∵EF=EM,CM=AF,
∴AF2+CE2=EF2.
点评:此题考查了全等三角形的判定与性质,线段垂直平分线性质,平行线的性质和判定的应用,此题图形变化很多,而且图形复杂,属于中等难度的题目,解题时要注意数形结合思想的应用.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案
相关题目
 如图,一位篮球运动员跳起投篮,球沿抛物线y=-0.2x2+3.5运行,然后准确落入篮筐内.已知篮筐的中心距离地面的距离为3.05米.
如图,一位篮球运动员跳起投篮,球沿抛物线y=-0.2x2+3.5运行,然后准确落入篮筐内.已知篮筐的中心距离地面的距离为3.05米. 如图,已知P、Q是△ABC的BC边上的两点,且BP=AP=AQ=QC,∠PAQ=60°.
如图,已知P、Q是△ABC的BC边上的两点,且BP=AP=AQ=QC,∠PAQ=60°. 如图,已知两条平行线AB,CD被直线EF所截,交点分别为G,H,P为HD上任意一点,由P向HF作射线OP,交点为O.
如图,已知两条平行线AB,CD被直线EF所截,交点分别为G,H,P为HD上任意一点,由P向HF作射线OP,交点为O.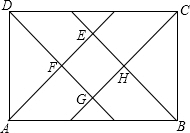 如图,在矩形ABCD中,AE、BE、CG、DG分别是各内角的平分线,E、F、G、H分别为它们的交点.求证:四边形EFGH是正方形.
如图,在矩形ABCD中,AE、BE、CG、DG分别是各内角的平分线,E、F、G、H分别为它们的交点.求证:四边形EFGH是正方形.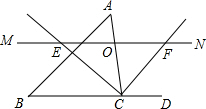 如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.