Question

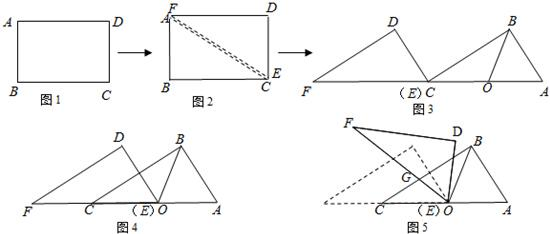
如图，现将一张矩形ABCD的纸片一角折叠，若能使点D落在AB边上F处，折痕为CE，恰好∠AEF=60°，延长EF交CB的延长线于点G．
（1）求证：△CEG是等边三角形；
（2）若矩形的一边AD=3，求另一边AB的长．

Answer 1

（1）证明：∵四边形ABCD是矩形，
∴AD∥BC即AD∥GC，
∴∠G=∠AEF=60°，
由折叠可知：∠CED=∠CEG，而∠GED=180°-∠AEF=120°
∴∠GEC=∠CED=∠GED=60°即∠G=∠GEC=60°，
∴△CEG是等边三角形；

（2）解：∵四边形ABCD是矩形∴∠A=∠D=90°，AB=CD，
由（1）可知∠AEF=∠CED=60°，∴∠AFE=∠DCE=30°，
∴EF=2AE，CE=2DE．设AE=x，则EF=2x，ED=EF=2x，
∴AD=x+2x=3，CE=4x，解得，x=1，DE=2，CE=4，
在Rt△CDE中，CD=
∴AB=2．
分析：（1）由折叠可知∠DEC=∠FEC，已知∠AEF=60°，可知∠DEC=∠FEC=60°，由AD∥GC，可知∠G=∠AEF=60°，故有∠G=∠FEC=60°，所以△CEG是等边三角形；
（2）在Rt△AEF中，∠AEF=60°，设AE=x，则EF=2x，由折叠的性质得ED=EF=2x，根据AE+ED=AD，列方程求x，在Rt△CDE中，DE=2，∠DEC=60°，可得CE=2DE=4，利用勾股定理可求CD，即AB的长．
点评：本题考查了折叠的性质及其运用．关键是由折叠求相等的线段，相等的角，把问题集中在直角三角形中使用勾股定理．