Question

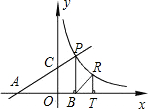
如图，在平面直角坐标系中，直线y=-

3

4

x+6交x轴于点A，交y轴于点B．点P，点Q同时从原点出发作匀速运动，点P沿x轴正方向运动，点Q沿OB→BA方向运动，并同时到达点A．点P运动的速度为1厘米/秒．
（1）求点Q运动的速度；
（2）当点Q运动到线段BA上时，设点P运动的时间为x（秒），△POQ的面积为y（平方厘米），那么用x的代数式表示AQ=______，并求y与x的函数关系式；
（3）若将（2）中所得函数的自变量x的取值范围扩大到任意实数后，其函数图象上是否存在点M，使得点M与该函数图象和x轴的两个交点所组成的三角形面积等于△AOB的面积？若存在，求出点M的坐标；若不存在，请说明理由．

Answer 1

（1）∵直线y=-34x+6交x轴于点A，交y轴于点B，
∴A（8，0），B（0，6）
∴OA=8，0B=6，AB=10
∴点Q运动的速度=（6+10）÷（8÷1）=2厘米/秒；

（2）AQ=10+6-2X=16-2X，
作QE⊥x轴于点E，则QE∥y轴，
∴△AQE∽△ABO
∴QE：6=AQ：AB
∴QE=

3

5

AQ
∴y=

1

2

•OP•QE=

1

2

•x•

3

5

（16-2x）=-

3

5

x 2+

24

5

x；

（3）设M（a，b）
令y=0，则0=-

3

5

x 2+

24

5

x
∴x=0或x=8
即函数图象与x轴交于（0，0），（8，6）
∵点M与该函数图象和x轴的两个交点所组成的三角形面积等于△AOB的面积
∴|b|×

1

2

×8=

1

2

×6×8
∴b=±6
当b=6时，6=-

3

5

x 2+

24

5

x，所以x=4±

6

；
当b=-6时，-6=-

3

5

x 2+

24

5

x，所以x=4±

26

．
所以M（4±

6

，6），（4±

26

，-6）．