Question

【题目】如图，四边形ABCD是平行四边形，对角线AC，BD相交于点O，且∠1=∠2．求证：四边形ABCD是矩形．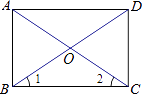

Answer 1

【答案】证明：在ABCD中，AO=CO，BO=DO， ∵∠1=∠2，
∴BO=CO，
∴AO=BO=CO=DO，
∴AC=BD，
∴ABCD为矩形
【解析】根据等角对等边得出OB=OC，根据平行四边形性质求出OC=OA= AC，OB=OD= BD，推出AC=BD，根据矩形的判定推出即可．
【考点精析】通过灵活运用平行四边形的性质和矩形的判定方法，掌握平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分；有一个角是直角的平行四边形叫做矩形；有三个角是直角的四边形是矩形；两条对角线相等的平行四边形是矩形即可以解答此题．