题目内容
为了从甲、乙两名学生中选拔一人参加今年六月份的全市中学生实验操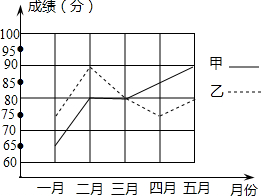 作竞赛,每个月对他们的实验水平进行一次测验.图给出两人赛前的5次测验成绩.
作竞赛,每个月对他们的实验水平进行一次测验.图给出两人赛前的5次测验成绩.(1)分别求出甲、乙两名学生5次测验成绩的平均数与方差;
(2)如果你是他们的辅导老师,应选派
分析:(1)根据折线图读出甲乙的数据,在根据平均数与方差的计算公式,计算出甲乙的方差与平均数;
(2)根据(1)的计算结果,先比较平均数的大小,再比较方差的大小,在平均数相等的情况下,找方差小,即成绩稳定的参加竞赛.
(2)根据(1)的计算结果,先比较平均数的大小,再比较方差的大小,在平均数相等的情况下,找方差小,即成绩稳定的参加竞赛.
解答:解:(1)由折线图可得:甲的5个数据依次为:65,80,80,85,90;乙的5个数据依次为:75,90,80,75,80;
故甲的平均数为
×(65+80+80+85+90)=80;
方差为
×(225+25+100)=70;
乙的平均数为
×(75+90+80+75+80)=80;
方差为
×(25+100+25)=30;
(2)根据(1)的计算结果,可得甲乙的平均数相等;但甲的方差比乙的方差大,即乙的成绩比甲的稳定;故应选乙参加这次竞赛.
故甲的平均数为
| 1 |
| 5 |
方差为
| 1 |
| 5 |
乙的平均数为
| 1 |
| 5 |
方差为
| 1 |
| 5 |
(2)根据(1)的计算结果,可得甲乙的平均数相等;但甲的方差比乙的方差大,即乙的成绩比甲的稳定;故应选乙参加这次竞赛.
点评:本题考查了平均数和方差的计算以及读折线图的能力和利用统计图获取信息的能力.

练习册系列答案
相关题目
为了从甲、乙两名学生中选择一人参加法律知识竞赛,在相同条件下对他们的法律知识进行了10次测验,成绩如下:(单位:分)
(1)请填写下表:
(2)利用(1)的信息分析,你认为选择哪位同学参赛比较合适,说明你的理由.
| 甲成绩 | 76 | 84 | 90 | 84 | 81 | 87 | 88 | 81 | 85 | 84 |
| 乙成绩 | 82 | 86 | 87 | 90 | 79 | 81 | 93 | 90 | 74 | 78 |
| 平均数 | 中位数 | 众数 | 方差 | |
| 甲 | 94 | 84 | 14.4 | |
| 乙 | 84 | 34 |