题目内容
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(0,3),且当x=1时,y有最小值2.
(1)求a,b,c的值
(2)设二次函数y=k(2x+2)﹣(ax2+bx+c)(k为实数),它的图象的顶点为D.
①当k=1时,求二次函数y=k(2x+2)﹣(ax2+bx+c)的图象与x轴的交点坐标;
②请在二次函数y=ax2+bx+c与y=k(2x+2)﹣(ax2+bx+c)的图象上各找出一个点M,N,不论k取何值,这两个点始终关于x轴对称,直接写出点M,N的坐标(点M在点N的上方);
③过点M的一次函数y=﹣![]() x+t的图象与二次函数y=ax2+bx+c的图象交于另一点P,当k为何值时,点D在∠NMP的平分线上?
x+t的图象与二次函数y=ax2+bx+c的图象交于另一点P,当k为何值时,点D在∠NMP的平分线上?
④当k取﹣2,﹣1,0,1,2时,通过计算,得到对应的抛物线y=k(2x+2)﹣(ax2+bx+c)的顶点分别为(﹣1,﹣6,),(0,﹣5),(1,﹣2),(2,3),(3,10),请问:顶点的横、纵坐标是变量吗?纵坐标是如何随横坐标的变化而变化的?
【答案】
(1)
解:设y=a(x﹣1)2+2,将(0,3)代入,得a=1,
∴y=(x﹣1)2+2,即y=x2﹣2x+3,
∴a=1,b=﹣2,c=3
(2)
解:①当k=1时,y=﹣x2+4x﹣1,令y=0,﹣x2+4x﹣1=0,解得x=2±![]() ,即图象与x轴的交点坐标(2+
,即图象与x轴的交点坐标(2+![]() ,0),(2﹣
,0),(2﹣![]() ,0);
,0);
②y=k(2x+2)﹣(ax2+bx+c)当经x=﹣1时,y=ax2+bx+c与y=k(2x+2)﹣(ax2+bx+c)的图象上点M,N,不论k取何值,这两个点始终关于x轴对称,
∴M(﹣1,6),N(﹣1,﹣6),
③y=﹣![]() x+t,经过(﹣1,6),得t=
x+t,经过(﹣1,6),得t=![]() ,
,
∴y=﹣![]() x+
x+![]() ,则A(7,0),
,则A(7,0),
∵MN⊥x轴,
∴E点的横坐标为﹣1,
∴AE=8,
∵ME=6,
∴MA=10.
如图1,设MD交AE于点B,作BC⊥AM于点C,
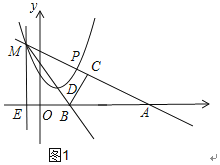
∵MD平分∠NMP,MN⊥x轴,
∴BC=BE,设BC=x,则AB=8﹣x,显然△ABC∽△AME,
∴![]() =
=![]() ,则x=3.得点B(2,0),
,则x=3.得点B(2,0),
∴MD的函数表达式为y=﹣2x+4.
∵y=ax2+bx+c与y=k(2x+2)﹣(ax2+bx+c)=﹣[x﹣(k+1)]2+(k+1)2+2k﹣3.
把D(k+1,k2+2k+1+2k﹣3),代入y=﹣2x+4.得k=﹣3±![]() ,
,
由y=k(2x+2)﹣(ax2+bx+c)有意义可得k=﹣3+![]() ,
,
④是.
当顶点的横坐标大于﹣1时,纵坐标随横坐标的增大而增大,
当顶点的横坐标小于﹣1时,纵坐标随横坐标的增大而减小.
【解析】(1)利用顶点式的解析式求解即可;
(2))①当k=1时,y=﹣x2+4x﹣1,令y=0,﹣x2+4x﹣1=0,解得x的值,即可得出图象与x轴的交点坐标;
②y=k(2x+2)﹣(ax2+bx+c)当经x=﹣1时,y=ax2+bx+c与y=k(2x+2)﹣(ax2+bx+c)的图象上点M,N,不论k取何值,这两个点始终关于x轴对称,可得M(﹣1,6),N(﹣1,﹣6);
③由y=﹣![]() +t,经过(﹣1,6),可得t的值,由MN⊥x轴,可得E点的横坐标为﹣1,可得出AE,ME,MA的值.设MD交AE于点B,作BC⊥AM于点C,设BC=x,则AB=8﹣x,显然△ABC∽△AMN,可求出x的值,即可得出MD的函数表达式为y=﹣2x+4.再把点D代入,即可求出k的值;
+t,经过(﹣1,6),可得t的值,由MN⊥x轴,可得E点的横坐标为﹣1,可得出AE,ME,MA的值.设MD交AE于点B,作BC⊥AM于点C,设BC=x,则AB=8﹣x,显然△ABC∽△AMN,可求出x的值,即可得出MD的函数表达式为y=﹣2x+4.再把点D代入,即可求出k的值;
④观察可得出当顶点的横坐标大于﹣1时,纵坐标随横坐标的增大而增大,当顶点的横坐标小于﹣1时,纵坐标随横坐标的增大而减小.

 名校课堂系列答案
名校课堂系列答案




