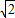题目内容
下列问题中,不正确的是
- A.两圆半径分别是4cm和2cm,一条外公切线长为4cm,则两圆位置关系为相交
- B.PA切⊙O于A,PAB为⊙O的割线,如果PB=2.PC=4,则PA的长为2

- C.如果⊙O1、⊙O2半径分别为4、5,当O1O2>6时,⊙O1与⊙O2必有公共点
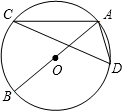
- D.AB是⊙O的直径,∠ACD=15°,则∠BAD的度数为75°
C
分析:A、求出两圆心之间的距离,再根据这个距离与两圆半径之和大小确定两圆位置关系;
B、根据切割线定理得PA2=PB•PC=8,即可求得PA的长;
C、根据圆与圆的位置关系即可求解;
D、由AB是圆的直径,则∠ADB=90°,由圆周角定理知,∠B=∠C=15°,即可求∠BAD=90°-∠B=75°.
解答: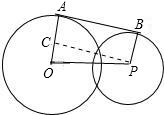 解:A、如图:
解:A、如图:
设两圆圆心分别为O和P,外公切线为AB,过P点作AB平行线交OA于C.
∵AB=4
∴PC=4
∵AO=4,PB=2
∴AC=2,OC=4-2=2.
在RT△CPO中
OP=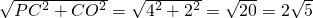 <4+2=6.
<4+2=6.
∴两圆位置关系为相交,正确;
 B、∵PA2=PB•PC=8,
B、∵PA2=PB•PC=8,
∵PB=2,PC=4,
∴PA=2 ,正确;
,正确;
C、当O1O2>9时,⊙O1与⊙O2没有公共点,错误;
D、∵AB是圆的直径,
∴∠ADB=90°,
∴∠B=∠C=15°,
∴∠BAD=90°-∠B=75°,正确.
点评:本题考查圆与圆的位置关系,切割线定理的运用,直径对的圆周角定理是直角和圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半,考查了学生的综合应用能力及推理能力.
分析:A、求出两圆心之间的距离,再根据这个距离与两圆半径之和大小确定两圆位置关系;
B、根据切割线定理得PA2=PB•PC=8,即可求得PA的长;
C、根据圆与圆的位置关系即可求解;
D、由AB是圆的直径,则∠ADB=90°,由圆周角定理知,∠B=∠C=15°,即可求∠BAD=90°-∠B=75°.
解答:
 解:A、如图:
解:A、如图:设两圆圆心分别为O和P,外公切线为AB,过P点作AB平行线交OA于C.
∵AB=4
∴PC=4
∵AO=4,PB=2
∴AC=2,OC=4-2=2.
在RT△CPO中
OP=
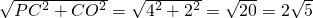 <4+2=6.
<4+2=6.∴两圆位置关系为相交,正确;
 B、∵PA2=PB•PC=8,
B、∵PA2=PB•PC=8,∵PB=2,PC=4,
∴PA=2
 ,正确;
,正确;C、当O1O2>9时,⊙O1与⊙O2没有公共点,错误;
D、∵AB是圆的直径,
∴∠ADB=90°,
∴∠B=∠C=15°,
∴∠BAD=90°-∠B=75°,正确.
点评:本题考查圆与圆的位置关系,切割线定理的运用,直径对的圆周角定理是直角和圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半,考查了学生的综合应用能力及推理能力.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 4、某校开展“了解传统习俗,弘扬民族文化”为主题的实践活动.实践小组就“是否知道端午节的来由”这个问题,对部分学生进行了调查,调查结果如图,其中不知道的学生有8人.下列说法不正确的是( )
4、某校开展“了解传统习俗,弘扬民族文化”为主题的实践活动.实践小组就“是否知道端午节的来由”这个问题,对部分学生进行了调查,调查结果如图,其中不知道的学生有8人.下列说法不正确的是( )