题目内容
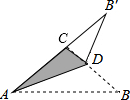 如图,已知△ABC中,∠CAB=∠B=30°,AB=2
如图,已知△ABC中,∠CAB=∠B=30°,AB=2| 3 |
考点:翻折变换(折叠问题)
专题:
分析:首先过点D作DE⊥AB′于点E,过点C作CF⊥AB,由△ABC中,∠CAB=∠B=30°,AB=2
,利用等腰三角形的性质,即可求得AC的长,又由折叠的性质,易得∠CDB′=90°,∠B′=30°,B′C=AB′-AC=2
-2,继而求得CD与B′D的长,然后求得高DE的长,继而求得答案.
| 3 |
| 3 |
解答: 解:过点D作DE⊥AB′于点E,过点C作CF⊥AB,
解:过点D作DE⊥AB′于点E,过点C作CF⊥AB,
∵△ABC中,∠CAB=∠B=30°,AB=2
,
∴AC=BC,
∴AF=
AB=
,
∴AC=
=
=2,
由折叠的性质得:AB′=AB=2
,∠B′=∠B=30°,
∵∠B′CD=∠CAB+∠B=60°,
∴∠CDB′=90°,
∵B′C=AB′-AC=2
-2,
∴CD=
B′C=
-1,B′D=B′C•cos∠B′=(2
-2)×
=3-
,
∴DE=
=
=
,
∴S阴影=
AC•DE=
×2×
=
.
故答案为:
.
 解:过点D作DE⊥AB′于点E,过点C作CF⊥AB,
解:过点D作DE⊥AB′于点E,过点C作CF⊥AB,∵△ABC中,∠CAB=∠B=30°,AB=2
| 3 |
∴AC=BC,
∴AF=
| 1 |
| 2 |
| 3 |
∴AC=
| AF |
| cos∠CAB |
| ||||
|
由折叠的性质得:AB′=AB=2
| 3 |
∵∠B′CD=∠CAB+∠B=60°,
∴∠CDB′=90°,
∵B′C=AB′-AC=2
| 3 |
∴CD=
| 1 |
| 2 |
| 3 |
| 3 |
| ||
| 2 |
| 3 |
∴DE=
| CD•B′D |
| B′C |
(
| ||||
2
|
3-
| ||
| 2 |
∴S阴影=
| 1 |
| 2 |
| 1 |
| 2 |
3-
| ||
| 2 |
3-
| ||
| 2 |
故答案为:
3-
| ||
| 2 |
点评:此题考查了折叠的性质,等腰三角形的性质、直角三角形的性质以及特殊角的三角函数问题.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用,注意掌握折叠前后图形的对应关系.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案
相关题目
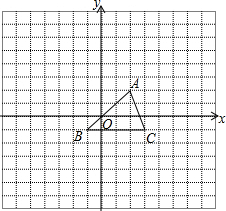 如图,方格纸中的每个小方格都是边长为1的正方形,我们把顶点在网格交点上的三角形称为“格点三角形”,图中的△ABC是格点三角形.在建立平面直角坐标系后,点A的坐标为(2,2).
如图,方格纸中的每个小方格都是边长为1的正方形,我们把顶点在网格交点上的三角形称为“格点三角形”,图中的△ABC是格点三角形.在建立平面直角坐标系后,点A的坐标为(2,2). 如图坡度:AB的坡度iAB=
如图坡度:AB的坡度iAB=