题目内容
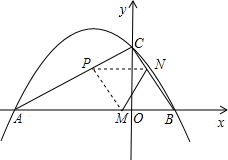
二次函数y=ax2+bx+c过点A、B两点(A左B右),且分布在y轴两侧,且OA、OB的长是方程x2-5x+4=0的两根,且OA>OB,与y轴交于点C(0,4).
(1)求4a-2b+c的值;
(2)连接AC、BC,P是线段AB上一动点,且AP=m,过点P作PM∥AC,交BC于M,当m为何值时,S△PCM的面积最大,并求出这个最大值;
(3)△ABC外接圆的面积是________.(直接写出答案,结果保留π)
(1)解:∵OA、OB的长是方程x2-5x+4=0的两根,且OA>OB,
∴OA=4,OB=1,
∵二次函数y=ax2+bx+c过点A、B两点(A左B右),且分布在y轴两侧,
∴A(-4,0),B(1,0),设抛物线的解析式是y=a(x-1)(x+4),
把C(0,4)代入得:4=a(0-1)(0+4),
a=-1,
∴y=-(x-1)(x+4)=-x2-3x+4,
4a-2b+c=4×(-1)-2×(-3)+4=6,
答:4a-2b+c的值是6;
(2)解:∵AP=m,
∴PB=5-m,
∵PM∥AC,
∴△PBM∽△ABC,
∴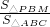 =
= ,
,
又∵S△ABC=10,
∴S△PBM=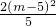 ,
,
又∵S△PCB=2(5-m),
∴S△PCM=10-2m-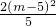 =-
=-
 +
+ ,
,
∴当m= 时,△PCM的面积最大,最大值是
时,△PCM的面积最大,最大值是 ,
,
答:当m为 时,S△PCM的面积最大,这个最大值是
时,S△PCM的面积最大,这个最大值是 .
.
(3)故答案为: .
.
分析:(1)根据OA、OB的长是方程x2-5x+4=0的两根,且OA>OB,求出OA=4,OB=1,得到A(-4,0),B(1,0),设抛物线的解析式是y=a(x-1)(x+4),把C(0,4)代入求出a=-1,得到抛物线的解析式y=-x2-3x+4,即可求出答案;
(2)由PM∥AC,得到△PBM∽△ABC,求出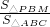 =
= ,根据三角形的面积公式得到S△ABC=10,求出S△PBM=
,根据三角形的面积公式得到S△ABC=10,求出S△PBM=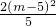 ,由S△PCB=2(5-m),求出S△PCM=10-2m-
,由S△PCB=2(5-m),求出S△PCM=10-2m-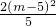 配方成顶点式即可求出答案;
配方成顶点式即可求出答案;
(3)设外接圆的圆心O(- ,y),根据OA=OC,求出y=
,y),根据OA=OC,求出y= ,根据勾股定理求出半径是
,根据勾股定理求出半径是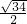 ,根据圆的面积公式即可求出答案.
,根据圆的面积公式即可求出答案.
点评:本题主要考查对相似三角形的性质和判定,三角形的面积,勾股定理,二次函数的最值,用待定系数法求二次函数的解析式,解一元二次方程,圆的面积,三角形的外接圆与外心等知识点的理解和掌握,综合运用这些性质进行计算是解此题的关键,此题是一个综合性比较强的题目,难度适中.
∴OA=4,OB=1,
∵二次函数y=ax2+bx+c过点A、B两点(A左B右),且分布在y轴两侧,
∴A(-4,0),B(1,0),设抛物线的解析式是y=a(x-1)(x+4),
把C(0,4)代入得:4=a(0-1)(0+4),
a=-1,
∴y=-(x-1)(x+4)=-x2-3x+4,
4a-2b+c=4×(-1)-2×(-3)+4=6,
答:4a-2b+c的值是6;
(2)解:∵AP=m,
∴PB=5-m,
∵PM∥AC,
∴△PBM∽△ABC,
∴
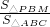 =
= ,
,又∵S△ABC=10,
∴S△PBM=
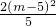 ,
,又∵S△PCB=2(5-m),
∴S△PCM=10-2m-
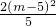 =-
=-
 +
+ ,
,∴当m=
 时,△PCM的面积最大,最大值是
时,△PCM的面积最大,最大值是 ,
,答:当m为
 时,S△PCM的面积最大,这个最大值是
时,S△PCM的面积最大,这个最大值是 .
.(3)故答案为:
 .
.分析:(1)根据OA、OB的长是方程x2-5x+4=0的两根,且OA>OB,求出OA=4,OB=1,得到A(-4,0),B(1,0),设抛物线的解析式是y=a(x-1)(x+4),把C(0,4)代入求出a=-1,得到抛物线的解析式y=-x2-3x+4,即可求出答案;
(2)由PM∥AC,得到△PBM∽△ABC,求出
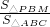 =
= ,根据三角形的面积公式得到S△ABC=10,求出S△PBM=
,根据三角形的面积公式得到S△ABC=10,求出S△PBM=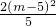 ,由S△PCB=2(5-m),求出S△PCM=10-2m-
,由S△PCB=2(5-m),求出S△PCM=10-2m-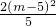 配方成顶点式即可求出答案;
配方成顶点式即可求出答案;(3)设外接圆的圆心O(-
 ,y),根据OA=OC,求出y=
,y),根据OA=OC,求出y= ,根据勾股定理求出半径是
,根据勾股定理求出半径是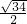 ,根据圆的面积公式即可求出答案.
,根据圆的面积公式即可求出答案.点评:本题主要考查对相似三角形的性质和判定,三角形的面积,勾股定理,二次函数的最值,用待定系数法求二次函数的解析式,解一元二次方程,圆的面积,三角形的外接圆与外心等知识点的理解和掌握,综合运用这些性质进行计算是解此题的关键,此题是一个综合性比较强的题目,难度适中.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
 点C
点C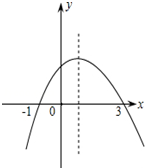 如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①abc>0;②2a+b=0;③a+b+c>0;④当-1<x<3时,y>0.其中正确结论的序号是
如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①abc>0;②2a+b=0;③a+b+c>0;④当-1<x<3时,y>0.其中正确结论的序号是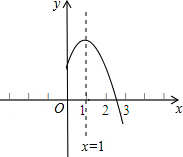 (2012•孝感)二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的对称轴是直线x=1,其图象的一部分如图所示.对于下列说法:
(2012•孝感)二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的对称轴是直线x=1,其图象的一部分如图所示.对于下列说法: