题目内容
【题目】如图,△ABC中,AB=AC=![]() ,cosC=
,cosC=![]() .
.

(1)动手操作:利用尺规作以AC为直径的⊙O,并标出⊙O与AB的交点D,与BC的交点E(保留作图痕迹,不写作法);
(2)综合应用:在你所作的图中,
①求证:弧DE=弧CE ;②求点D到BC的距离.
【答案】(1)作图见解析;(2)①证明见解析;②![]() .
.
【解析】试题分析:(1)先作出AC的中垂线,再画圆;
(2)边接AE,AE是BC的中垂线,∠DAE=∠CAE,得出 DE=CE,
(3)利用△BDE∽△BCA求出BD,再利用余弦求出BM,用勾股定理求出DM.
试题解析:(1)如图,
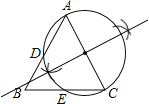
(2)如图,连接AE,
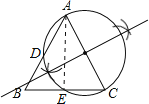
∵AC为直径,∴∠AEC=90°,
∵AB=AC,∴∠DAE=∠CAE,
∴ DE=CE .
(3)如图,连接AE,DE,作DM⊥BC交BC于点M,
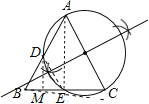
∵AC为直径,∴∠AEC=90°,
∵AB=AC= 4![]() ,cosC=
,cosC= ![]() ,∴EC=BE=4,∴BC=8,
,∴EC=BE=4,∴BC=8,
∵点A、D、E、C共圆,∴∠ADE+∠C=180°,
又∵∠ADE+∠BDE=180°,∴∠BDE=∠C,∴△BDE∽△BCA,
∴![]() 即BD
即BD![]() BA=BE
BA=BE![]() BC,∴BD×4
BC,∴BD×4![]() =4×8,
=4×8,
∴BD= ![]() ,
,
∵∠B=∠C,∴cos∠C=cos∠B=![]() ,
,
∴ ![]() ,∴BM=
,∴BM= ![]() ,
,
∴DM= ![]() .
.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目