题目内容
 23、看图填空:
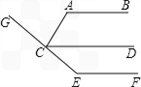
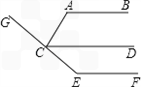
23、看图填空:如图,AB∥CD∥EF,FG过点G,∠A=120°,∠E=145°,
求:∠ACG的度数.
解:∵AB∥CD(已知)
∴∠
CAB
+∠ACD
=180°又∵∠A=120°
∴∠ACD=
60°
.∵CD∥EF(已知)
∴∠
CEF
+∠ECD
=180°又∵∠E=145°
∴∠ECD=
35°
.∵∠
GCA
+∠ACD
+∠ECD
=180°∴∠ACG=
85°
.分析:由AB∥CD,根据平行线的性质得到∠CAB+∠ACD=180°,∠CEF+∠ECD=180°,可分别求出∠ACD,∠ECD,然后利用平角的定义计算出∠ACG即可.
解答:解:故答案为:CAB,ACD,60°,CEF,ECD,35°,GCA,ACD,ECD,85°.
点评:本题考查了平行线的性质:两直线平行,同旁内角互补;也考查了平角的定义.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
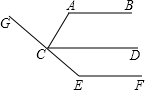 求:∠ACG的度数.
求:∠ACG的度数.