题目内容
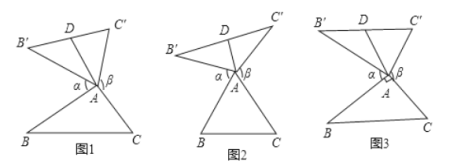
【题目】将正方形ABCD和正方形BEFG如图(一)所示放置,已知AB=5![]() ,BE=6,将正方形BEFG绕点B顺时针旋转一定的角度α(0°≤α≤360°)到图(二)所示:连接AE,CG,
,BE=6,将正方形BEFG绕点B顺时针旋转一定的角度α(0°≤α≤360°)到图(二)所示:连接AE,CG,
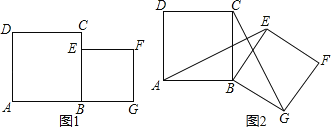
(1)求线段AE与CG的关系,并给出证明
(2)当旋转至某一个角度时,点C,E,G在同一条直线上,请画出示意图形,并求出此时AE的长
【答案】(1)AE=CG,证明详见解析;(2)AE=![]() 或
或![]()
【解析】
(1)由旋转中对应边和对应角相等,可证△ABE≌△CBG,可得AE=CG
(2)画图可知,点C、E、G在同一条直线上存在两种情况,根据(1)的全等证明,可知AE=CG,利用CG所在三角形利用勾股定理求出CH,加上HG可得CG长度即AE的长.
解:(1)AE=AG
∵AB=CB,∠ABE=∠CBG,BE=BG
∴△ABE≌△CBG(SAS)
∴AE=CG
(2)当E在CG线段上时,如图所示
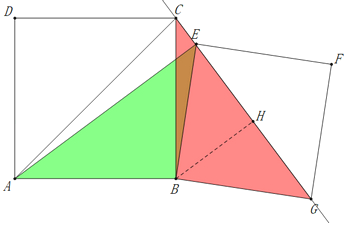
由(1)可知△ABE≌△CBG
∴AE=CG
在Rt△CBH中
BC=![]() ,BH=EH=
,BH=EH=![]()
∴CH=![]()
∴CE=![]()
∴CG=![]()
∴AE=![]()
当点E在CG的延长线上时,如图所示

由(1)可知△ABE≌△CBG
∴AE=CG
在Rt△BHC中
BH=HG=![]() ,BC=
,BC=![]()
∴CH=![]()
∴CG=![]()
∴AE=![]()
∴AE=![]() 或
或![]()

【题目】商场销售某种冰箱,该种冰箱每台进价为2500元.已知原销售价为每台2900元时,平均每天能售出8台.若在原销售价的基础上每台降价50元,则平均每天可多售出4台.设每台冰箱的实际售价比原销售价降低了x元.
(1)填表(不需化简):
每天的销售量/台 | 每台销售利润/元 | |
降价前 | 8 | 400 |
降价后 |
(2)商场为使这种冰箱平均每天的销售利润达到5000元,则每台冰箱的实际售价应定为多少元?
【题目】如图,是一张平行四边形纸片ABCD,要求利用所学知识作出一个菱形,甲、乙两位同学的作法分别如下:
甲:连接AC,作AC的中垂线交AD、BC于E、F,则四边形AFCE是菱形. | 乙:分别作 |
对于甲、乙两人的作法,可判断( )

A.甲正确,乙错误B.甲错误,乙正确
C.甲、乙均正确D.甲、乙均错误