题目内容
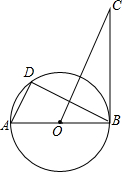已知如图，AB是⊙O的直径，BC⊥AB于B，D是⊙O上的一点，且AD∥OC．（1）求证：△ADB∽△OBC；
（2）若AO=2，BC=2
| 2 |
分析：（1）根据平行线的性质得∠A=∠COB，根据直径所对的圆周角是直角得∠D=∠OBC，就可以判定△ADB∽△OBC；
（2）根据相似三角形的对应边成比例可以计算出OC的长．
（2）根据相似三角形的对应边成比例可以计算出OC的长．
解答：解：（1）∵AD∥OC，∴∠A=∠COB．
AB是直径，∴∠D=∠OBC=90°，∴△ADB∽△OBC．
（2）∵AO=2，BC=2
，
∴OC=2
又∵△ADB∽△OBC，
∴
=
，即
=
，OC=2
，
∴AD=
．
AB是直径，∴∠D=∠OBC=90°，∴△ADB∽△OBC．
（2）∵AO=2，BC=2
| 2 |
∴OC=2
| 3 |
又∵△ADB∽△OBC，
∴
| AD |
| OB |
| AB |
| OC |
| AD |
| 2 |
| 4 | ||
2
|
| 3 |
∴AD=
4
| ||
| 3 |
点评：本题难度中等，考查相似三角形的判定和性质．
练习册系列答案
名校课堂系列答案
相关题目
6、已知如图，AB是⊙O的直径，弦CD⊥AB于E，CD=6，AE=1，则⊙O的直径为（ ）
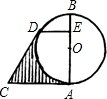已知如图，AB是⊙O直径，∠C的两边分别与⊙O相切于A、D两点．DE⊥AB，垂足为E，AE=3，BE=1，则图中阴影部分面积（ ）A、4
| ||||||
B、
| ||||||
C、
| ||||||
D、4
|
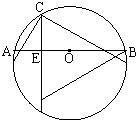19、已知如图，AB是⊙O的直径，AB垂直弦CD于点E，则在不添加辅助线的情况下，图中与∠CDB相等的角是
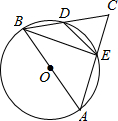已知如图：AB是⊙O的直径，AB=AC，BC交⊙O于点D，AC交⊙O于点E，∠BAC=45°，给出以下四个结论：（1）∠EBC=22.5°（2）BD=DC；（3）