题目内容
 如图,直线y=-
如图,直线y=-| 3 | 4 |
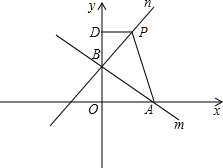
(1)求点A、B的坐标;
(2)若△ABO与△BDP全等,试求直线n的函数解析式;
(3)将△ABP沿直线m对折,点P恰好与点O重合,试求点P的坐标.
分析:(1)对于直线m,令x与y分别为0求出对应y与x的值,即可确定出A与B的坐标;
(2)分两种情况考虑:当△BDP≌△AOB时,BD=AO=4,DP=BO=3,由OB+BD求出OD的长,得到P的坐标,设直线n为y=kx+b,将B与P坐标代入得到关于k与b的方程组,求出方程组的解得到k与b的值,即可求出此时直线n解析式;当△PDB≌△AOB时,BD=OB=3,PD=OA=4,由OB+BD求出OD的长,求出P的坐标,设直线n为y=mx+n,将B与P代入得到关于m与n的方程组,求出方程组的解得到m与n的值,即可确定出直线n的解析式;
(3)过O与P作直线OP,与AB交于点Q,将△ABP沿直线m对折,点P恰好与点O重合时,△AOB≌△APB,可得出BO=BP,OA=PA,进而确定出AB垂直平分线段OP,由直线AB的斜率求出直线OP的斜率,求出直线OP的解析式,与直线AB解析式联立求出Q的坐标,由Q为线段OP的中点,利用中点坐标公式即可求出P的坐标.
(2)分两种情况考虑:当△BDP≌△AOB时,BD=AO=4,DP=BO=3,由OB+BD求出OD的长,得到P的坐标,设直线n为y=kx+b,将B与P坐标代入得到关于k与b的方程组,求出方程组的解得到k与b的值,即可求出此时直线n解析式;当△PDB≌△AOB时,BD=OB=3,PD=OA=4,由OB+BD求出OD的长,求出P的坐标,设直线n为y=mx+n,将B与P代入得到关于m与n的方程组,求出方程组的解得到m与n的值,即可确定出直线n的解析式;
(3)过O与P作直线OP,与AB交于点Q,将△ABP沿直线m对折,点P恰好与点O重合时,△AOB≌△APB,可得出BO=BP,OA=PA,进而确定出AB垂直平分线段OP,由直线AB的斜率求出直线OP的斜率,求出直线OP的解析式,与直线AB解析式联立求出Q的坐标,由Q为线段OP的中点,利用中点坐标公式即可求出P的坐标.
解答: 解:(1)对于直线y=-
解:(1)对于直线y=-
x+3,令x=0,得到y=3;令y=0,得到x=4,
则A(4,0),B(0,3);
(2)当△BDP≌△AOB时,BD=AO=4,DP=BO=3,
∴OD=OB+BD=3+4=7,
∴P(3,7),
设直线n为y=kx+b,将B与P坐标代入得:
,
解得:
,
此时直线n解析式为y=
x+3;
当△PDB≌△AOB时,BD=OB=3,PD=OA=4,
∴OB+BD=3+3=6,
∴P(4,6),
设直线n为y=mx+n,将B与P代入得:
,
解得:
,
此时直线n解析式为y=
x+3;
(3)过O与P作直线OP,与AB交于点Q,
将△ABP沿直线m对折,点P恰好与点O重合时,△AOB≌△APB,
∴BO=BP,OA=PA,
∴直线AB垂直平分线段OP,
∵直线AB解析式为y=-
x+3,斜率为-
,
∴直线OP斜率为
,即直线OP解析式为y=
x,
联立两函数解析式得:
,
解得:
,
∴Q(
,
),
∵Q为线段OP的中点,
∴P(
,
).
 解:(1)对于直线y=-
解:(1)对于直线y=-| 3 |
| 4 |
则A(4,0),B(0,3);
(2)当△BDP≌△AOB时,BD=AO=4,DP=BO=3,
∴OD=OB+BD=3+4=7,
∴P(3,7),
设直线n为y=kx+b,将B与P坐标代入得:
|
解得:
|
此时直线n解析式为y=
| 4 |
| 3 |
当△PDB≌△AOB时,BD=OB=3,PD=OA=4,
∴OB+BD=3+3=6,
∴P(4,6),
设直线n为y=mx+n,将B与P代入得:
|
解得:
|
此时直线n解析式为y=
| 3 |
| 4 |
(3)过O与P作直线OP,与AB交于点Q,
将△ABP沿直线m对折,点P恰好与点O重合时,△AOB≌△APB,
∴BO=BP,OA=PA,
∴直线AB垂直平分线段OP,
∵直线AB解析式为y=-
| 3 |
| 4 |
| 3 |
| 4 |
∴直线OP斜率为
| 4 |
| 3 |
| 4 |
| 3 |
联立两函数解析式得:
|
解得:
|
∴Q(
| 36 |
| 25 |
| 48 |
| 25 |
∵Q为线段OP的中点,
∴P(
| 72 |
| 25 |
| 96 |
| 25 |
点评:此题属于一次函数综合题,涉及的知识有:直线与坐标轴的交点,待定系数法求一次函数解析式,两直线的交点,折叠的性质,以及线段中点坐标公式,是一道中档题.

练习册系列答案
相关题目
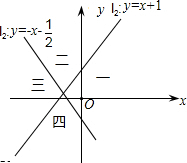 如图,直线l1:y=x+1与直线l2:y=-x-
如图,直线l1:y=x+1与直线l2:y=-x-| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| 2 |
| A、第一部分 | B、第二部分 |
| C、第三部分 | D、第四部分 |
 14、如图,直线AB、CD交于O点,OE为∠AOC的平分线,∠1=17°,则∠2=
14、如图,直线AB、CD交于O点,OE为∠AOC的平分线,∠1=17°,则∠2=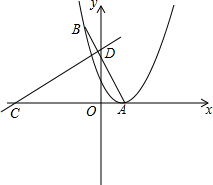 (2012•江汉区模拟)已知:抛物线
(2012•江汉区模拟)已知:抛物线 (2009•无锡二模)如图,直线L1∥L2,AB⊥CD,∠1=34°,那么∠2的度数是
(2009•无锡二模)如图,直线L1∥L2,AB⊥CD,∠1=34°,那么∠2的度数是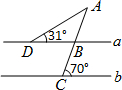 (2012•广州模拟)如图,直线a∥b,则∠A的度数是( )
(2012•广州模拟)如图,直线a∥b,则∠A的度数是( )