题目内容
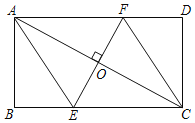
【题目】如图,平行四边形ABCD中,AB∶BC=3∶2,∠DAB=60°,E在AB上,且AE∶EB=1∶2,F是BC的中点,过D分别作DP⊥AF于P,DQ⊥CE于Q,则DP∶DQ等于
A.3∶4 B.![]() ∶
∶![]() C.
C.![]() ∶
∶![]() D.
D.![]() ∶
∶![]()
【答案】D
【解析】
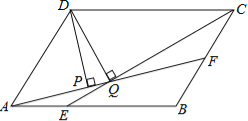
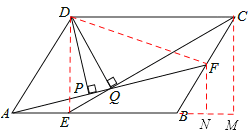
连接DE、DF,过F作FN⊥AB于N,过C作CM⊥AB于M,
∵根据三角形的面积和平行四边形的面积得:
![]() ,即
,即![]() 。
。
∴AF×DP=CE×DQ,。
∵四边形ABCD是平行四边形,∴AD∥BC。
∵∠DAB=60°,∴∠CBN=∠DAB=60°。∴∠BFN=∠MCB=30°。
∵AB:BC=3:2,∴设AB=3a,BC=2a。
∵AE:EB=1:2,F是BC的中点,∴BF=a,BE=2a,BN=![]() a,BM=a。
a,BM=a。
由勾股定理得:FN=![]() a,CM=
a,CM=![]() a。
a。
∴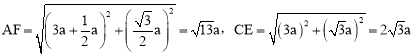 。
。
∴![]() 。∴
。∴![]() 。故选D。
。故选D。

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
【题目】为了解某社区居民的用电情况,随机对该社区10户居民进行调查,下表是这10户居民2018年4月份用电量的调查结果:
居民(户) | 1 | 2 | 3 | 4 |
月用电量(度) | 30 | 42 | 50 | 51 |
那么关于这10户居民月用电量(单位:度),下列说法错误的是( )
A. 中位数是50度 B. 众数是51度
C. 方差是42度2 D. 平均数是46.8度