题目内容
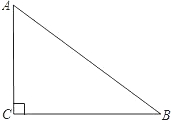 如图所示,已知:Rt△ABC中,∠ACB=90°.
如图所示,已知:Rt△ABC中,∠ACB=90°.(1)尺规作图:作∠BAC的平分线AM交BC于点D(只保留作图痕迹,不写作法);
(2)在(1)所作图形中,将Rt△ABC沿某条直线折叠,使点A与点D重合,折痕EF交AC于点E,交AB于点F,连接DE、DF,再展回到原图形,得到四边形AEDF.
①试判断四边形AEDF的形状,并证明;
②若AC=8,CD=4,求四边形AEDF的周长和BD的长.
分析:(1)按作角的平分线步骤作即可;
(2)由题意和已知可知EF是线段AD的垂直平分线,AD是∠BAC的平分线,再证明△AEG≌△AFG,易得四边相等,所以四边形AEDF是菱形;②在Rt△ECD中,根据勾股定理求得DE的值,则AE=DE,即可求得周长;求BD的长,可证明△BFD∽△BAC,根据比例线段求得.
(2)由题意和已知可知EF是线段AD的垂直平分线,AD是∠BAC的平分线,再证明△AEG≌△AFG,易得四边相等,所以四边形AEDF是菱形;②在Rt△ECD中,根据勾股定理求得DE的值,则AE=DE,即可求得周长;求BD的长,可证明△BFD∽△BAC,根据比例线段求得.
解答: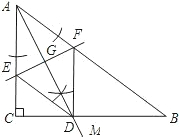 解:(1)如图,(1分)
解:(1)如图,(1分)
写出结论:射线AM就是所要求的角平分线;(2分)
(2)①四边形AEDF是菱形.(3分)
证明:如图,
根据题意,可知EF是线段AD的垂直平分线,
则AE=ED,AF=FD,∠AGE=∠AGF=90°,
由(1)可知,AD是∠BAC的平分线,
∴∠EAD=∠DAF.
∵∠AGE=∠AGF,AG=AG,
∴△AEG≌△AFG.(4分)
∴AE=AF∴AE=ED=DF=AF.
∴四边形AEDF是菱形.(5分)
②设AE=x,则ED=x,CE=8-x,
在Rt△ECD中,42+(8-x)2=x2,
解得x=5,∴4x=20.
即四边形AEDF的周长是20.(7分)
由①可知,四边形AEDF是菱形,
∴FD∥AC,
∴△BFD∽△BAC,
∴
=
,(8分)
∴
=
,
解得BD=
.
即BD的长是
.(10分)
 解:(1)如图,(1分)
解:(1)如图,(1分)写出结论:射线AM就是所要求的角平分线;(2分)
(2)①四边形AEDF是菱形.(3分)
证明:如图,
根据题意,可知EF是线段AD的垂直平分线,
则AE=ED,AF=FD,∠AGE=∠AGF=90°,
由(1)可知,AD是∠BAC的平分线,
∴∠EAD=∠DAF.
∵∠AGE=∠AGF,AG=AG,
∴△AEG≌△AFG.(4分)
∴AE=AF∴AE=ED=DF=AF.
∴四边形AEDF是菱形.(5分)
②设AE=x,则ED=x,CE=8-x,
在Rt△ECD中,42+(8-x)2=x2,
解得x=5,∴4x=20.
即四边形AEDF的周长是20.(7分)
由①可知,四边形AEDF是菱形,
∴FD∥AC,
∴△BFD∽△BAC,
∴
| BD |
| BC |
| DF |
| AC |
∴
| BD |
| BD+4 |
| 5 |
| 8 |
解得BD=
| 20 |
| 3 |
即BD的长是
| 20 |
| 3 |
点评:本题考查图形的折叠与拼接,同时考查了三角形、四边形等几何基本知识,解题时应分别对每一个图形进行仔细分析.

练习册系列答案
相关题目
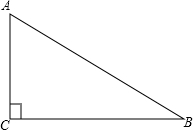 如图所示,已知:Rt△ABC中,∠ACB=90°.
如图所示,已知:Rt△ABC中,∠ACB=90°.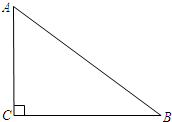 如图所示,已知:Rt△ABC中,∠ACB=90°.
如图所示,已知:Rt△ABC中,∠ACB=90°.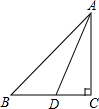 如图所示,已知:Rt△ABC中,∠C=90°,AC=BC,AD是∠A的平分线.
如图所示,已知:Rt△ABC中,∠C=90°,AC=BC,AD是∠A的平分线. 如图所示,已知在Rt△ABC中,∠C=90°,BC=4,AC=4,现将△ABC沿射线CB方向平移到△A′B′C′的位置.若平移距离为3,求△ABC与△A′B′C′的重叠部分的面积.
如图所示,已知在Rt△ABC中,∠C=90°,BC=4,AC=4,现将△ABC沿射线CB方向平移到△A′B′C′的位置.若平移距离为3,求△ABC与△A′B′C′的重叠部分的面积.