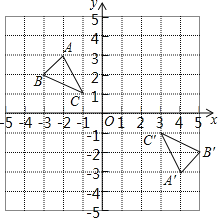
[题目]如图,在平面直角坐标系中,已知三个顶点的坐标分别是.(1)请在图中,画出绕着点逆时针旋转后得到的,则的正切值为 .(2)以点为位似中心,将缩小为原来的,得到,请在图中轴左侧,画出,若点是上的任意一点,则变换后的对应点的坐标是 . 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图,在平面直角坐标系中,已知三个顶点的坐标分别是.

(1)请在图中,画出绕着点逆时针旋转后得到的,则的正切值为 .

(2)以点为位似中心,将缩小为原来的,得到,请在图中轴左侧,画出,若点是上的任意一点,则变换后的对应点的坐标是 .

【答案】（1）图详见解析，；（2）图详见解析，变换后的对应点的坐标是.

【解析】

1）依据旋转的方向、角度和旋转中心，即可得到△ABC绕着点O逆时针旋转90°后得到的△A1B1C1，进而得到∠A1C1B1的正切值；.

（2）依据点O为位似中心，将△ABC缩小为原来的，即可得到△A2B2C2，以及变换后的对应点P′的坐标．

(1)如图所示,即为所求；由题可得，；

(2)如图所示,即为所求，

∵点是上的任意一点，点为位似中心，

∴变换后的对应点的坐标是.

练习册系列答案

（1）二等奖的获奖人数所占的百分比是　；

（2）在此次比赛中，一共有多少同学参赛？请将折线统计图补充完整．

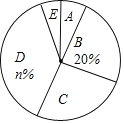
【题目】某校为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况，随机选取该校部分学生进行调查，要求每名学生从中只选一类最喜爱的电视节目，以下是根据调查结果绘制的统计图表的一部分．

类别	A	B	C	D	E
节目类型	新闻	体育	动画	娱乐	戏曲
人数	12	30	m	54	9

请你根据以上的信息，回答下列问题：

（1）被调查的学生中，最喜爱体育节目的有　　人，这些学生数占被调查总人数的百分比为　　%．

（2）被调查学生的总数为　　人，统计表中m的值为　　，统计图中n的值为　　．

（3）在统计图中，E类所对应扇形圆心角的度数为　　．

（4）该校共有2000名学生，根据调查结果，估计该校最喜爱新闻节目的学生数．

【题目】数轴上的A、B、C三点所表示的数分别为a、b、1，且|a﹣1|+|b﹣1|＝|a﹣b|，则下列选项中，满足A、B、C三点位置关系的数轴为（　　）

A. B.

C. D.

【题目】如图，一辆轿车在经过某路口的感应线B和C处时，悬臂灯杆上的电子警察拍摄到两张照片，两感应线之间距离BC为6m，在感应线B、C两处测得电子警察A的仰角分别为∠ABD＝18°，∠ACD＝14°．求电子警察安装在悬臂灯杆上的高度AD的长．

（参考数据：sin14°≈0.242，cos14°≈0.97，tan14°≈0.25，sin18°≈0.309，cos18°≈0.951，tan18°≈0.325）

【题目】（问题引入）

如图（1），在中，，，过作则交延长线于点，则易得

（直接应用）

如图,已知等边的边长为,点, 分别在边, 上, , 为中点，为当上一动点，当在何处时，与相似，求的值.

（拓展应用）

已知在平行四边形中，，，，,，求长.

【题目】联想三角形外心的概念，我们可引入如下概念。

定义：到三角形的两个顶点距离相等的点，叫做此三角形的准外心。

举例：如图1，若PA=PB，则点P为△ABC的准外心。

应用：如图2，CD为等边三角形ABC的高，准外心P在高CD上，且PD=AB，求∠APB的度数。

探究：已知△ABC为直角三角形，斜边BC=5，AB=3，准外心P在AC边上，试探究PA的长。

【题目】我国古代数学的许多发现都曾位居世界前列，其中“杨辉三角”就是一例．如图，这个三角形的构造法则：两腰上的数都是1，其余每个数均为其上方左、右两数之和，它给出了（a+b）n（n为正整数）的展开式（按a的次数由大到小的顺序排列）的系数规律．例如，在三角形中第三行的三个数1，2，1，恰好对应（a+b）2＝a2+2ab+b2展开式中的系数；第四行的四个数1，3，3，1，恰好对应着（a+b）3＝a3+3a2b+3ab2+b2展开式中的系数等．

（1）（a+b）n展开式中项数共有　　项．

（2）写出（a+b）5的展开式：（a+b）5＝　　．

（3）利用上面的规律计算：25﹣5×24+10×23﹣10×22+5×2﹣1．

【题目】如图，在平面直角坐标系中，△ABC的顶点坐标为A（﹣2，3），B（﹣3，2），C（﹣1，1）．

（1）若将△ABC向右平移3个单位长度，再向上平移1个单位长度，请画出平移后的△A1B1C1；

（2）画出△A1B1C1绕原点顺时针旋90°后得到的△A2B2C2；

（3）若△A′B′C′与△ABC是中心对称图形，则对称中心的坐标为．

试题分类