题目内容
(本题12分)已知两直线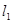 ,
,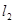 分别经过点A(3,0),点B(-1,0),并且当两直线同时相交于y负半轴的点C时,恰好有
分别经过点A(3,0),点B(-1,0),并且当两直线同时相交于y负半轴的点C时,恰好有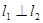 ,经过点A、B、C的抛物线的对称轴与直线
,经过点A、B、C的抛物线的对称轴与直线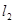 交于点D,如图所示。
交于点D,如图所示。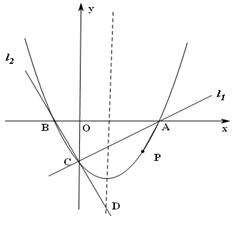
(1)求抛物线的函数解析式;
(2)当直线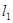 绕点C顺时针旋转一个锐角时,它与抛物线的另一个交点为P(x,y),求四边形APCB面积S关于x的函数解析式,并求S的最大值;
绕点C顺时针旋转一个锐角时,它与抛物线的另一个交点为P(x,y),求四边形APCB面积S关于x的函数解析式,并求S的最大值;
(3)当直线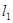 绕点C旋转时,它与抛物线的另一个交点为P,请找出使△PCD为等腰三角形的点P,并求出点P的坐标。
绕点C旋转时,它与抛物线的另一个交点为P,请找出使△PCD为等腰三角形的点P,并求出点P的坐标。
(1)可由两角相等证得:△BOC∽△COA。
得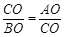 ,即
,即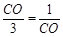 ,
,
∴ ,
,
∴C(0,- )
)
设 ,把(0,-
,把(0,- )代入,得a=
)代入,得a=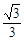 ,
,
∴抛物线的函数解析式为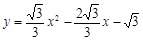
(2)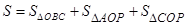
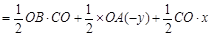
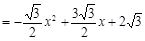 (0<x<3)
(0<x<3)
当x=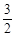 时,S的最大值是
时,S的最大值是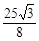
(3)可得直线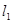 为
为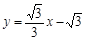 ,直线
,直线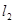 为
为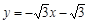 ,
,
抛物线的对称轴为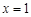 ,抛物线顶点为(1,
,抛物线顶点为(1,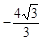 ),由此得D(1,
),由此得D(1,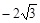 )
)
① 以点D为圆心,线段DC长为半径画弧,交抛物线于点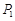 ,由抛物线对称性可知点
,由抛物线对称性可知点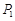 为点C关于直线
为点C关于直线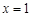 的对称点,
的对称点,
∴点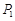 (2,
(2,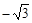 ),此时△
),此时△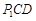 为等腰三角形;
为等腰三角形;
② 当以点C为圆心,线段CD长为半径画弧时,与抛物线交点为点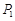 和点B,而三点B、C、D在同一直线上,不能构成三角形;
和点B,而三点B、C、D在同一直线上,不能构成三角形;
③ 作线段DC的中垂线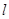 ,交CD于点M,交抛物线于点P2,P3,交y轴于点F,
,交CD于点M,交抛物线于点P2,P3,交y轴于点F,
因为BO=1, ,所以∠MCF=∠OCB=30°,
,所以∠MCF=∠OCB=30°,
而CD=2,CM=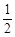 CD=1,则CF=
CD=1,则CF=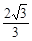 ,OF=
,OF=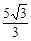 ,
,
则F(0,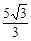 ),因
),因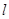 ∥
∥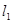 ,所以直线
,所以直线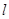 为
为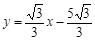 ,
,
代入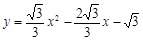 ,解得x=1或x=2,
,解得x=1或x=2,
说明P2就是顶点(1,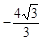 ),
),
P3就是P1(2,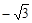 )
)
综上所述,当点P为(-2, )或(1,
)或(1,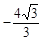 )时,△PCD为等腰三角形。
)时,△PCD为等腰三角形。
解析试题分析:(1)由两组底脚相等,推导出两个三角形相似,从而确立C点坐标,再结合AB两点的坐标,可以求得二次函数解析式。
(2)由于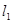 绕C点运动,因此P的坐标设为(x,y),四边形面积可以写为
绕C点运动,因此P的坐标设为(x,y),四边形面积可以写为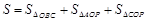 ,
,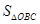 无未知量,
无未知量,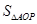 和
和 可以由的高分别为-y和x,又P点为抛物线上一点,所以可以算出y和x的关系式,进而求出S与x的函数式。由于解出来的函数为二次函数,x的取值范围已知,求出函数对称轴,得出函数对称轴在此范围内,所以要求最大值,实际上则是代入对称轴所对应的x值,可得出S。
可以由的高分别为-y和x,又P点为抛物线上一点,所以可以算出y和x的关系式,进而求出S与x的函数式。由于解出来的函数为二次函数,x的取值范围已知,求出函数对称轴,得出函数对称轴在此范围内,所以要求最大值,实际上则是代入对称轴所对应的x值,可得出S。
(3)通过分类讨论,各种不同的情况所对应的等腰三角形也不相同,由已知条件可以推导出两条直线的方程,结合函数图像,可以得出P点的坐标。
考点:函数图像;几何图形
点评:一般试卷最后一道题都是综合性的题目,学生需要掌握几何图形以及函数图形、函数表达式的知识,从而将复杂的题目简单化,进而可以求出一些未知量。

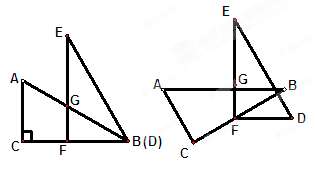
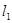 ,
, 分别经过点A(3,0),点B(-1,0),并且当两直线同时相交于y负半轴的点C时,恰好有
分别经过点A(3,0),点B(-1,0),并且当两直线同时相交于y负半轴的点C时,恰好有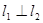 ,经过点A、B、C的抛物线的对称轴与直线
,经过点A、B、C的抛物线的对称轴与直线
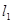 绕点C顺时针旋转一个锐角时,它与抛物线的另一个交点为P(x,y),求四边形APCB面积S关于x的函数解析式,并求S的最大值;
绕点C顺时针旋转一个锐角时,它与抛物线的另一个交点为P(x,y),求四边形APCB面积S关于x的函数解析式,并求S的最大值;