题目内容
如图,我们称每个小正方形的顶点为“格点”,以格点为顶点的三角形叫做“格点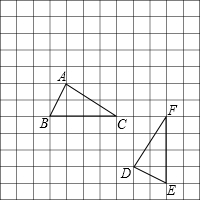 三角形”.根据图形解答下列问题:
三角形”.根据图形解答下列问题:
(1)图中的格点△DEF是由格点△ABC通过怎样的变换得到的?(写出变换过程)
(2)在图中建立适当的直角坐标系,写出△DEF各顶点的坐标.
解:(1)答案不唯一,只要合理即可得.如:
将△ABC向右平移3个格得到△A1B1C1,再将△A1B1C1以点C1为旋转中心,按逆时针方向旋转90°就得到了△DEF;
(2)答案不唯一,只要正确建立直角坐标系并正确写出各点坐标,即可得.如:
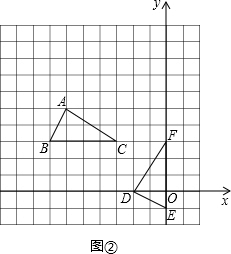
方法一:如图①建立直角坐标系,则点D(0,0)、E(2,-1)、F(2,3);
方法二:如图②建立直角坐标系,则点D(-2,0)、E(0,-1)、F(0,3);
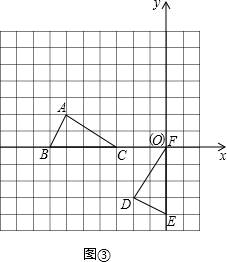
方法三:如图③建立直角坐标系,则点D(-2,-3)、E(0,-4)、F(0,0);
方法四:如图④建立直角坐标系,则点D(-2,1)、E(0,0)、F(0,4).


分析:(1)对应点是C、F,△ABC应先以点C为基准向右平移到F,BC转到EF位置,可看出是逆时针旋转90°,
(2)可任意建立平面直角坐标系,得到相应三点的坐标.
点评:图形的转换应找到关键点,关键线段的变化,原点位置不同,得到点的坐标也不同.
将△ABC向右平移3个格得到△A1B1C1,再将△A1B1C1以点C1为旋转中心,按逆时针方向旋转90°就得到了△DEF;
(2)答案不唯一,只要正确建立直角坐标系并正确写出各点坐标,即可得.如:
方法一:如图①建立直角坐标系,则点D(0,0)、E(2,-1)、F(2,3);
方法二:如图②建立直角坐标系,则点D(-2,0)、E(0,-1)、F(0,3);
方法三:如图③建立直角坐标系,则点D(-2,-3)、E(0,-4)、F(0,0);
方法四:如图④建立直角坐标系,则点D(-2,1)、E(0,0)、F(0,4).




分析:(1)对应点是C、F,△ABC应先以点C为基准向右平移到F,BC转到EF位置,可看出是逆时针旋转90°,
(2)可任意建立平面直角坐标系,得到相应三点的坐标.
点评:图形的转换应找到关键点,关键线段的变化,原点位置不同,得到点的坐标也不同.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
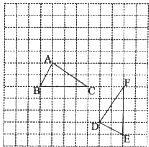 10、如图,我们称每个小正方形的顶点为“格点”,以格点为顶点的三角形叫做“格点三角形”.根据图形解答下列问题:
10、如图,我们称每个小正方形的顶点为“格点”,以格点为顶点的三角形叫做“格点三角形”.根据图形解答下列问题: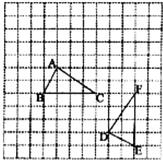 (1)计算:
(1)计算:

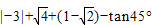 ;
; ;
;