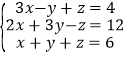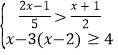题目内容
【题目】如图，已知EC∥AB，∠EDA=∠ABF．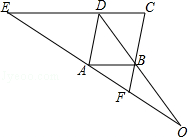 
（1）求证：四边形ABCD是平行四边形；
（2）求证：OA2=OEOF．
【答案】
（1）证明：∵EC∥AB，
∴∠EDA=∠DAB，
∵∠EDA=∠ABF，
∴∠DAB=∠ABF，
∴AD∥BC，
∵DC∥AB，
∴四边形ABCD为平行四边形
（2）证明：∵EC∥AB，
∴△OAB∽△OED，
∴ 
= 
，
∵AD∥BC，
∴△OBF∽△ODA，
∴ = 
，
∴ = ，
∴OA2=OEOF
【解析】（1）由EC∥AB，∠EDA=∠ABF，可证得∠DAB=∠ABF，即可证得AD∥BC，则得四边形ABCD为平行四边形；（2）由EC∥AB，可得 = ，由AD∥BC，可得 = ，等量代换得出 = ，即OA2=OEOF．
练习册系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
【题目】希望中学八年级学生开展踢毽子活动，每班派5名学生参加，按团体总分排列名次，在规定时间内每人踢100个以上（含100）为优秀．下表是成绩较好的甲班和乙班5名学生的比赛成绩（单位：个）
1号 | 2号 | 3号 | 4号 | 5号 | 总数 | |
甲班 | 100 | 98 | 110 | 89 | 103 | 500 |
乙班 | 89 | 100 | 95 | 119 | 97 | 500 |
经统计发现两班5名学生踢毽子的总个数相等．此时有学生建议，可以通过考查数据中的其它信息作为参考．请你回答下列问题：
（1）求两班比赛数据的中位数；
（2）计算两班比赛数据的方差，并比较哪一个小；
（3）根据以上信息，你认为应该把冠军奖状发给哪一个班？简述理由.
