题目内容
【题目】在![]() ,
,![]() ,
,![]() ,高
,高![]() ,则BC的长是( )
,则BC的长是( )
A.14B.4C.4或14D.7或13
【答案】C
【解析】
分两种情况讨论:锐角三角形和钝角三角形,根据勾股定理求得BD,CD,再由图形求出BC,在锐角三角形中,BC=BD+CD,在钝角三角形中,BC=CDBD.
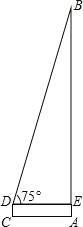
解:(1)如图
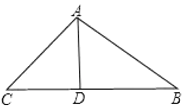
锐角△ABC中,AB=15,AC=13,BC边上高AD=12,
在Rt△ABD中AB=15,AD=12,由勾股定理得:
BD2=AB2AD2=152122=81,
∴BD=9,
在Rt△ACD中AC=13,AD=12,由勾股定理得
CD2=AC2AD2=132122=25,
∴CD=5,
∴BC的长为BD+DC=9+5=14;
(2)如图
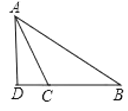
钝角△ABC中,AB=15,AC=13,BC边上高AD=12,
在Rt△ABD中AB=15,AD=12,由勾股定理得:
BD2=AB2AD2=152122=81,
∴BD=9,
在Rt△ACD中AC=13,AD=12,由勾股定理得:
CD2=AC2AD2=132122=25,
∴CD=5,
∴BC的长为DCBD=95=4.
故BC长为14或4.
故选:C.

练习册系列答案
相关题目