题目内容
圆的直径为12,如果直线与圆相交,且直线与圆心的距离为d,则d满足( )A.d<6
B.6<d<12
C.d=6
D.d>12
【答案】分析:根据直线与圆相交时d<r,根据答案分别分析即可.
解答:解:∵直线与圆相交,
∴直线与圆心的距离为d<r,
∵r=6,∴d<6.
故选:A.
点评:此题主要考查了直线与圆的位置关系,根据题意得出直线圆相交时d<r是解决问题的关键.
解答:解:∵直线与圆相交,
∴直线与圆心的距离为d<r,
∵r=6,∴d<6.
故选:A.
点评:此题主要考查了直线与圆的位置关系,根据题意得出直线圆相交时d<r是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
(本题满分12分)在平面直角坐标系中,抛物线交 轴于
轴于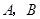 两点,交
两点,交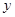 轴于点
轴于点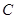 ,已知抛物线的对称轴为
,已知抛物线的对称轴为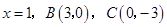 .
.
【小题1】⑴求这个抛物线的解析式;
【小题2】⑵在抛物线的对称轴上是否存在一点 ,使点
,使点 到A、C两点间的距离之和最大.若存在,求出点
到A、C两点间的距离之和最大.若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【小题3】(3)如果在 轴上方平行于
轴上方平行于 轴的一条直线交抛物线于
轴的一条直线交抛物线于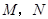 两点,以
两点,以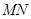 为直径作圆恰好与
为直径作圆恰好与 轴相切,求此圆的直径.
轴相切,求此圆的直径.
 轴于
轴于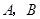 两点,交
两点,交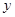 轴于点
轴于点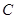 ,已知抛物线的对称轴为
,已知抛物线的对称轴为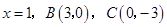 .
. |
【小题1】⑴求这个抛物线的解析式;
【小题2】⑵在抛物线的对称轴上是否存在一点
 ,使点
,使点 到A、C两点间的距离之和最大.若存在,求出点
到A、C两点间的距离之和最大.若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.【小题3】(3)如果在
 轴上方平行于
轴上方平行于 轴的一条直线交抛物线于
轴的一条直线交抛物线于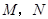 两点,以
两点,以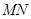 为直径作圆恰好与
为直径作圆恰好与 轴相切,求此圆的直径.
轴相切,求此圆的直径. (本题满分12分)在平面直角坐标系中,抛物线交 轴于
轴于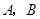 两点,交
两点,交 轴于点
轴于点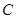 ,已知抛物线的对称轴为
,已知抛物线的对称轴为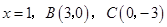 .
.
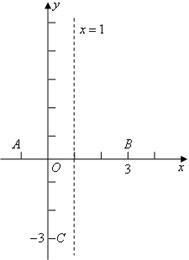 |
【小题1】⑴求这个抛物线的解析式;
【小题2】⑵在抛物线的对称轴上是否存在一点
 ,使点
,使点 到A、C两点间的距离之和最大.若存在,求出点
到A、C两点间的距离之和最大.若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.【小题3】(3)如果在
 轴上方平行于
轴上方平行于 轴的一条直线交抛物线于
轴的一条直线交抛物线于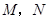 两点,以
两点,以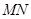 为直径作圆恰好与
为直径作圆恰好与 轴相切,求此圆的直径.
轴相切,求此圆的直径.