题目内容
我县农业结构调整取得了巨大成功,今年水果又喜获丰收.某乡组织30辆汽车装运A、B、C三种水果共64吨到外地销售,规定每辆汽车只装运一种水果,且必须装满;又装运每种水果的汽车不少于4辆.设用x辆汽车装运A种水果,用y辆汽车装运B种水果.
(1)用含x、y的式子表示装运C种水果的车辆数;
(2)根据下表提供的信息,求y与x之间的函数关系式;
| 水果品种 | A | B | C |
| 每辆汽车装运量(吨) | 2.2 | 2.1 | 2 |
| 每吨水果获利(百元) | 6 | 8 | 5 |
(4)试一试,请你写出自变量的取值范围,并提出一个获得最大利润时的车辆分配方案.
解:(1)30-x-y;
(2)由题得到:2.2x+2.1y+2(30-x-y)=64,
所以y=-2x+40;
(3)Q=0.06×2.2x+0.08×2.1y+0.05×2(30-x-y),
=0.032x+0.068y+3,
=0.032x+0.068(-2x+40)+3,
=-0.104x+5.72;
(4)由题意得,2.2x+2.1y+2(30-x-y)=64,所以y=-2x+40.
由题意可知:x≥4,-2x+40≥4,30-x-(-2x+40)≥4,
∴2.1(-2x+40)≤64-2.1(-2x+40),
∴x≥4,x≤18,x≥14,x≥12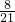 ,
,
∴14≤x≤18.
Q= [6×2.2x+8×2.1y+5+2(30-x-y)]=-0.104x+5.72.
[6×2.2x+8×2.1y+5+2(30-x-y)]=-0.104x+5.72.
当Q最大时,xmin=14,y=-2x+40=12,
C种水果车辆数为30-12-14=4.
故运A种水果需要14辆,B种需要12辆,C种需要4辆.
分析:(1)直接根据题意列式即可;
(2)利用表格中的数据和“A、B、C三种水果共64吨”列出方程变形后可得y与x之间的函数关系式;
(3)利用利润的求算方法写出Q=0.06×2.2x+0.08×2.1y+0.05×2(30-x-y)=0.032x+0.068y+3.
(4)首先依题意列出x与y的等式2.2x+2.1y+2(30-x-y)=64,然后根据题意求出x与y的取值范围.再根据x,y关于Q的函数表达式求解.
点评:本题主要考查利用函数的模型解决实际问题的能力.要先根据题意列出函数关系式,再代数求值.解题的关键是要分析题意根据实际意义求解.注意:数学应用题来源于实践用于实践,在当今社会市场经济的环境下,应掌握一些有关商品价格和利润的知识,总利润等于总收入减去总成本,然后再利用二次函数求最值.
(2)由题得到:2.2x+2.1y+2(30-x-y)=64,
所以y=-2x+40;
(3)Q=0.06×2.2x+0.08×2.1y+0.05×2(30-x-y),
=0.032x+0.068y+3,
=0.032x+0.068(-2x+40)+3,
=-0.104x+5.72;
(4)由题意得,2.2x+2.1y+2(30-x-y)=64,所以y=-2x+40.
由题意可知:x≥4,-2x+40≥4,30-x-(-2x+40)≥4,
∴2.1(-2x+40)≤64-2.1(-2x+40),
∴x≥4,x≤18,x≥14,x≥12
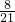 ,
,∴14≤x≤18.
Q=
 [6×2.2x+8×2.1y+5+2(30-x-y)]=-0.104x+5.72.
[6×2.2x+8×2.1y+5+2(30-x-y)]=-0.104x+5.72.当Q最大时,xmin=14,y=-2x+40=12,
C种水果车辆数为30-12-14=4.
故运A种水果需要14辆,B种需要12辆,C种需要4辆.
分析:(1)直接根据题意列式即可;
(2)利用表格中的数据和“A、B、C三种水果共64吨”列出方程变形后可得y与x之间的函数关系式;
(3)利用利润的求算方法写出Q=0.06×2.2x+0.08×2.1y+0.05×2(30-x-y)=0.032x+0.068y+3.
(4)首先依题意列出x与y的等式2.2x+2.1y+2(30-x-y)=64,然后根据题意求出x与y的取值范围.再根据x,y关于Q的函数表达式求解.
点评:本题主要考查利用函数的模型解决实际问题的能力.要先根据题意列出函数关系式,再代数求值.解题的关键是要分析题意根据实际意义求解.注意:数学应用题来源于实践用于实践,在当今社会市场经济的环境下,应掌握一些有关商品价格和利润的知识,总利润等于总收入减去总成本,然后再利用二次函数求最值.

练习册系列答案
相关题目
我县农业结构调整取得了巨大成功,今年水果又喜获丰收.某乡组织30辆汽车装运A、B、C三种水果共64吨到外地销售,规定每辆汽车只装运一种水果,且必须装满;又装运每种水果的汽车不少于4辆.设用x辆汽车装运A种水果,用y辆汽车装运B种水果.
(1)用含x、y的式子表示装运C种水果的车辆数;
(2)根据下表提供的信息,求y与x之间的函数关系式;
(3)设此次外销活动的利润为Q(万元),求Q与x之间的函数关系式;
(4)试一试,请你写出自变量的取值范围,并提出一个获得最大利润时的车辆分配方案.
(1)用含x、y的式子表示装运C种水果的车辆数;
(2)根据下表提供的信息,求y与x之间的函数关系式;
| 水果品种 | A | B | C |
| 每辆汽车装运量(吨) | 2.2 | 2.1 | 2 |
| 每吨水果获利(百元) | 6 | 8 | 5 |
(4)试一试,请你写出自变量的取值范围,并提出一个获得最大利润时的车辆分配方案.

