Question

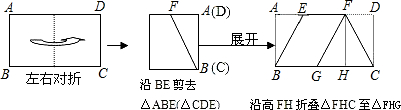
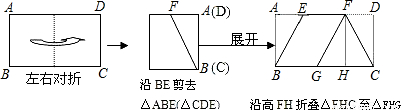
如图，将一张矩形纸ABCD按图示折叠：

（1）求证：四边形EFGB是平行四边形；
（2）若BC=11cm，AB=4cm，要使四边形EFGB为菱形，则剪去的△ABE的边AE应为多长？

Answer 1

（1）证明：由折叠知：△ABE≌△DCF，
∴BE=CF．
∵EF∥BC，且EF＜BC，
∴四边形BEFC为等腰梯形．
∴∠EBC=∠FCH．
∵∠FCH=∠FGC，
∴∠EBC=∠FGC．
∴EB∥FG．
又∵EF∥BG，
∴四边形EFGB是平行四边形．

（2）解：设AE=x，则DF=CH=GH=x，
∵四边形EFGB为菱形，
∴BE=EF=11-2x．
在Rt△ABE中，有4²+x²=（11-2x）²
化简得：3x²-44X+105=0．
解之得：x₁=3，x₂=＞11（舍去），
∴剪去的△ABE的边AE的长应为3cm．
分析：（1）由一组对边平行另一组对边相等可得到剪去后得到的四边形是等腰梯形．再次折叠后得到新四边形的另一组对边也平行，即可得证；
（2）综合利用勾股定理和邻边相等求解．
点评：本题用到的知识点为：两组对边分别平行的四边形是平行四边形；有一组邻边相等的平行四边形是菱形．
需注意折叠过程中得到的特殊四边形和特殊三角形的运用．