题目内容
【题目】某体育用品商店老板到体育商场批发篮球、足球、排球共![]() 个,得知该体育商场篮球、足球、排球平均每个
个,得知该体育商场篮球、足球、排球平均每个![]() 元,篮球比排球每个多
元,篮球比排球每个多![]() 元,排球比足球每个少
元,排球比足球每个少![]() 元.
元.
(1) 求出这三种球每个各多少元;
(2) 经决定,该老板批发了这三种球的任意两种共![]() 个,共花费了1060元,问该老板可能买了哪两种球?各买了几个;
个,共花费了1060元,问该老板可能买了哪两种球?各买了几个;
(3) 该老板打算将每一种球各提价![]() 元后,再进行打折销售,若排球、足球打八折,篮球打八五折,在(2)的情况下,为获得最大利润,他批发的一定是哪两种球?各买了几个?计算并说明理由.
元后,再进行打折销售,若排球、足球打八折,篮球打八五折,在(2)的情况下,为获得最大利润,他批发的一定是哪两种球?各买了几个?计算并说明理由.
【答案】(1)篮球每只40元,足球38元,排球30元;(2)若买的是足球和排球则求得可以是买足球20,排球10只;若买的是篮球和排球则是篮球16只,排球14只;(3)买篮球16只,排球14只利润最大.
【解析】
(1)分别设篮球每只x元,足球y,排球z,根据题意可得出三个二元一次不定方程,联立求解即可得出答案.
(2)假设:①买的是篮球和足球,分别为a只和b只,根据题意可得出两个方程,求出解后可判断出是否符合题意,进而再用同样的方法判断其他的符合题意的情况;
(3)分别对两种情况下的利润进行计算,然后比较利润的大小即可得出答案.
(1)设篮球每只x元,足球y,排球z,得
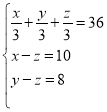 ;
;
解得x=40;y=38;z=30;
故篮球每只40元,足球38元,排球30元;
(2)假设:①买的是篮球和足球,分别为a只和b只,则
![]() ;
;
解得![]() ,则不可能是这种情况;
,则不可能是这种情况;
同理若买的是足球和排球则求得可以是买足球20,排球10只;
若买的是篮球和排球则是篮球16只,排球14只;
(3)对两种情况分别计算,若为足球和排球,即(38+20)×0.8×20+(30+20)0.8×10=1328(元);
若为篮球和排球,即(40+20)×0.85×16+(30+20)×0.8×14=1376(元),
∴买篮球16只,排球14只利润最大.

 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案【题目】某面包店推出一款新口味面包,每个成本1.5元,售价5元/个,试营业期间一律8折,每天只生产50个,为保持面包新鲜,当天未卖完的当天销毁,试营业期间市场日需求量(即每天所需数量)如表所示:
天数 | 8 | 10 | 10 | 2 |
日需求量/个 | 45 | 48 | 51 | 56 |
(1)补充日销售量(即每天销售的数量)的条形统计图;
(2)试营业期间某天的日需求量为45个,求当天的利润;
(3)求试营业期间(30)天的总利润