题目内容
如图,双曲线![]() 经过四边形OABC的顶点 A、C,∠ABC= 900,OC平分OA与x轴正半轴的夹角. AB//x轴,将∆ABC沿AC翻折后得△AB’C,点B’落在 OA上,则四边形OABC的面积是______
经过四边形OABC的顶点 A、C,∠ABC= 900,OC平分OA与x轴正半轴的夹角. AB//x轴,将∆ABC沿AC翻折后得△AB’C,点B’落在 OA上,则四边形OABC的面积是______
2
解析:延长BC,交x轴于点D,设点C(x,y),AB=a,
∵OC平分OA与x轴正半轴的夹角,∴CD=CB′,△OCD≌△OCB′,
再由翻折的性质得,BC=B′C,∵双曲线y= (x>0)经过四边形OABC的顶点A、C,
(x>0)经过四边形OABC的顶点A、C,
∴S△OCD=![]() xy=1,∴S△OCB′=
xy=1,∴S△OCB′=![]() xy=1,∵AB∥x轴,∴点A(x-a,2y),∴2y(x-a)=2,
xy=1,∵AB∥x轴,∴点A(x-a,2y),∴2y(x-a)=2,
∴xy-ay=1,∵xy=2 ∴ay=1, ∴S△ABC=![]() ay=
ay=![]() ,∴SOABC=S△OCB′+S△ABC+S△ABC=1+
,∴SOABC=S△OCB′+S△ABC+S△ABC=1+![]() +
+![]() =2.
=2.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
 经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与
经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与 轴正半轴的夹角,AB∥
轴正半轴的夹角,AB∥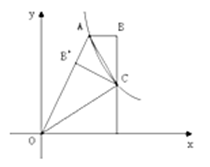
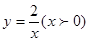 经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与
经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与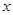 轴正半轴的夹角,AB∥
轴正半轴的夹角,AB∥
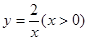 经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与
经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与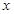 轴正半轴的夹角,AB∥
轴正半轴的夹角,AB∥
 经过四边形OABC的顶点 A、C,∠ABC= 900,OC平分OA与x轴正半轴的夹角. AB//x轴,将∆ABC沿AC翻折后得△AB’C,点B’落在 OA上,则四边形OABC的面积是______
经过四边形OABC的顶点 A、C,∠ABC= 900,OC平分OA与x轴正半轴的夹角. AB//x轴,将∆ABC沿AC翻折后得△AB’C,点B’落在 OA上,则四边形OABC的面积是______